Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{P}+\overrightarrow{Q}=m.\overrightarrow{a}\)
a)chiếu lên chiều chuyển động của thang máy
Q-P=m.a\(\Rightarrow\)Q=720N
b)Q-P=m.-a\(\Rightarrow\)Q=480N
c) chiều lên chiều chuyển động của thang( đi xuống)
-Q+P=m.a\(\Rightarrow\)\(\)Q=480N
d)Q=m.a+P=720N
e) thang máy rơi tự do (hướng xuống, a=10m/s2_
-Q+P=m.a\(\Rightarrow\)Q=0N

bài 1: Chọn chiều dương là chiều chuyển động, góc thời gian lúc xe 1 bắt đầu cđ.
pt cđ của xe 1: x1= v01.t + a1.t2/2 = 0,25.t2
pt cđ của xe 2: x1= v02.t = 10t
Khi xe 1 đuổi kịp xe 2: x1=x2 <=> 0,25.t2=10t <=> t = 40s
=> S1 = 0,25.402=400m ; v1 = 0,5.40 = 20 m/s
bài 2: Chọn chiều dương là chiều cđ, góc thời gian lúc xe ô tô khởi hành từ A.
ptvt xe 1: v1 = 0,5.t ; ptvt xe 2: v2 = 5 + 0,3t
ptcđ xe 1: x1 =-0,25.t2 ; ptcđ xe 2: x2 = -125 + 5t + 0,15.t2
a. gặp nhau <=> x1 = x2 <=>-0,25.t2 = -125 + 5t + 0,15.t2 <=> t = 18,3s
vị trí gặp nhau: |-0,25*t2| = 84m -> cách A 84m
v1 = ... ; v2 = ....
b. xe từ A -> B:-125 = -0,25.t2 <=> t = 10\(\sqrt{5}\)s => xe A đi được 125m
=>qđ xe từ B đi được: x2 = 61,8m

2) ta có : \(\left\{{}\begin{matrix}v_0+a\left(3-\frac{1}{2}\right)=8\\v_0+a\left(6-\frac{1}{2}\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_0+\frac{5}{2}a=8\\v_0+\frac{11}{2}a=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-3a=6\\v_0+\frac{5}{2}a=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-2\left(m/s^2\right)\\v_0=13m/s\end{matrix}\right.\)
=> Chọn D.
Bài1:
\(S_1=v_0.2-\frac{1}{2}.a2^2=20\)
=> \(2v_0-2a=60\)(1)
\(v^2-v_0^2=2as\Rightarrow0^2-v_0^2=2a.20\Rightarrow v_0=\sqrt{40a}\)(2)
Từ (1) và (2) => \(2.\sqrt{40a}-2a=60\)
=> \(2\left(\sqrt{40a}-a\right)=60\)
<=> \(\sqrt{40a}-a=30\)
<=> \(\sqrt{40a}=30+a\Leftrightarrow40a=a^2+60a+900\)
=> \(a^2+20a+900=0\) (pt vô nghiệm)

a) Khi thang máy đứng yên, lực kế chỉ trọng lượng thật của người:
![]()
b) Khi thang máy đi xuống nhanh dần đều:
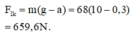
c) Khi thang máy đi xuống chậm dần đều:
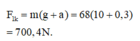



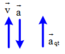

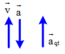


Ta có g → / = g → + a → q t mà trọng lượng của vật khi thang máy chuyển động là P / = m g /
a. Khi thang máy đứng yên a = 0 m / s 2
⇒ N = P = m g = 10.10 = 100 N
b. Đi lên nhanh dần đều với gia tốc 1 m / s 2
a → q t ↓ ↓ g → ⇒ g / = g + a q t
⇒ g / = 10 + 2 = 12 m / s 2 ⇒ N = P / = m g / = 10.12 = 120 N
c. Đi lên chậm dần đều với gia tốc 2 m / s 2
a → q t ↑ ↓ g → ⇒ g / = g − a q t
⇒ g / = 10 − 2 = 8 m / s 2 ⇒ N = P / = m g / = 10.8 = 80 N
d. Đi xuống nhanh dần đều với gia tốc 2 m / s 2
a → q t ↑ ↓ g → ⇒ g / = g − a q t
⇒ g / = 10 − 2 = 8 m / s 2 ⇒ N = P / = m g / = 10.8 = 80 N
e. Đi xuống chậm dần đều với gia tốc 2 m / s 2
a → q t ↓ ↓ g → ⇒ g / = g + a q t
⇒ g / = 10 + 2 = 12 m / s 2 ⇒ N = P / = m g / = 10.12 = 120 N
f. Chuyển động thẳng đều 2m/s
Vì thang máy chuyển động thẳng đều nên
a = 0 m / s 2 ⇒ N = P = m g = 10.10 = 100 N