Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

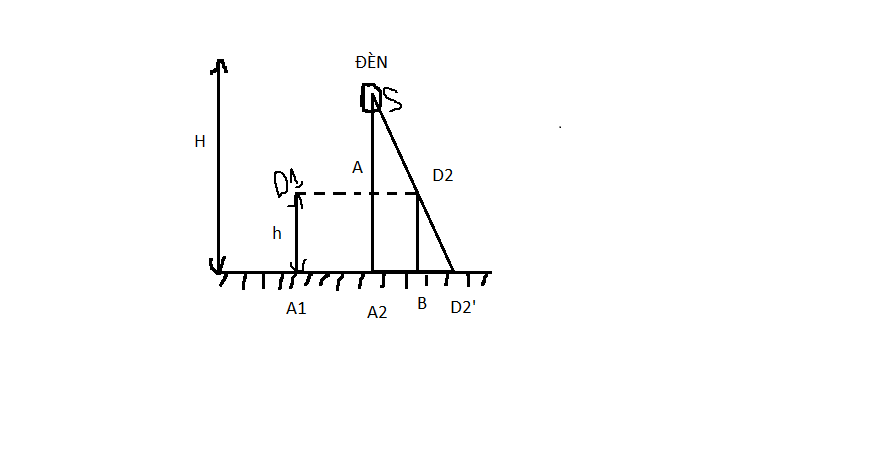
Các tia sáng bị chặn lại bởi người tạo ra một khoảng tối.
\(\Delta D_2BD_2'\)∼ \(\Delta SA_2D_2'\)
\(\Rightarrow\dfrac{BD_2'}{A_2D}=\dfrac{D_2D_2'}{SD_2'}\)
\(\Rightarrow D_2D_2'=SD_2'\cdot\dfrac{BD_2'}{A_2D}=x\cdot\dfrac{h}{H}\)
Xét trong khoảng thời gian t người đó dịch chuyển một đoạn \(S'=C_1C_2=v\cdot t\)
Bóng của đỉnh đầu dịch chuyển một đoạn \(x=C_1D_2'\)
Mà \(x=v\cdot t+x\cdot\dfrac{h}{H}=vt\cdot\dfrac{H}{H-h}\)
\(v'=\dfrac{x}{t}=v\cdot\dfrac{H}{H-h}\)

Nếu là xác định vận tốc thì giải như sau :
gọi vận tốc của bóng trên nền nhà là \(v_1\)
Xét sau một thời gian t
quãng đường mà đỉnh đầu người đi được la \(s=v.t\)
quãng đường mà cái bóng trên nền nhà đi được \(s_1=v_1.t\)
vẽ hình ra, từ thời điểm ban đầu đến thời điểm t sẽ tính được tỷ lệ dựa vào định lý talet trong tam giác. ta có kết quả là :
\(v_1=\dfrac{v.H}{H-h}\)

Tóm tắt:
a) Đã có thời gian rồi mà em, hay ý em là vận tốc?
t = 30 min = 0,5 h
S = 10 km
V = ?
b)
S' = 3000 m = 3 km
V' = 10 km/h
t' = ?
Giải
a) Vận tốc mà người đó đi hết quãng đường từ nhà đến sân bóng là:
\(V=\dfrac{S}{t}=\dfrac{10}{0,5}=20\) (km/h)
b) Thời gian mà người đó đi hết quãng đường là:
\(t'=\dfrac{S'}{V'}=\dfrac{3}{10}=0,3\left(h\right)\)