K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

BL
6 tháng 3 2020
A B H C B' C' I a b c D E d x
Gọi BD, CE là bóng của cọc và B',C' là đỉnh tương ứng của 2 cọc
Đặt \(BB'=CC'=a;BD=b;CE=c;BC=d;AH=x\)
Gọi I là giao điểm của AH và BC
\(\Rightarrow\frac{AI}{AH}=\frac{B'C'}{DE}\Rightarrow\frac{x-a}{a}=\frac{d}{b+d+c}\)
\(\Rightarrow\left(x-a\right)\left(b+d+c\right)=x.d\)
\(\Rightarrow x=\frac{ab+ad+ac}{b+c}=a\left(1+\frac{d}{b+c}\right)\)
Thay số ta được:\(AH=1,6\left(1+\frac{1,4}{0,4+0,6}\right)=3,84\left(m\right)\)
Vậy....

12 tháng 4 2023
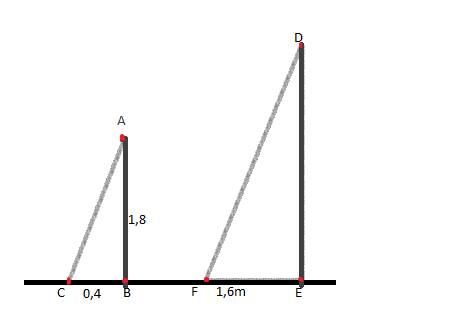
ΔDEF đồng dạng với ΔABC
=>DE/AB=EF/BC
=>DE/1,8=1,6/0,4
=>DE=7,2(m)
bạn ơi những mình tính có hai đáp số là AH = 12,8 m hoặc AH = 3,84 m