Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

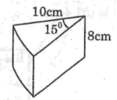
Thể tích khối pho mát hình trụ là :
\(\pi.10^2.8=800\pi\left(cm^3\right)\)
Thể tích mẩu pho mát bằng \(\dfrac{15^0}{360^0}=\dfrac{1}{24}\) thể tích khối pho mát
Khối lượng mẩu pho mát là :
\(\dfrac{1}{24}.800\pi.3=100\pi\left(g\right)\)
Vậy chọn (B)

Thể tích khối pho mát hình trụ :
V = π . 10 2 .8 = 800 π ( c m 3 )
Thể tích mẩu pho mát bằng 15/360 =1/24 thể tích khối pho mát
Khối lượng mẩu pho mát : m = (1/24) .800 π .3 = 100 π (g)
Vậy thể tích mẫu pho mát là:

Vậy chọn đáp án B

Gọi khối lượng riêng của miếng kim loại thứ nhất là: x (g/cm3 )
Khối lượng riêng của miếng kim loại thứ hai là: x - 1 (g/cm3 )
Thể tích của miếng kim loại thứ nhất là: (cm3 )
Thể tích của miếng kim loại thứ hai là: (cm3 )
Theo đầu bài ta có phương trình: -
= 10
Giải phương trình:
10x(x - 1) = 858x - 880x + 880 hay 5x2 + 6x - 440 = 0
∆' =9 + 2200 = 2209, √∆' = 47
x1 = 8,8, x2 = -10
Vì x > 0 nên x2 = -10 (loại)
Trả lời: Khối lượng riêng của miếng kim loại thứ nhất là: 8,8 g/cm3
Khối lượng riêng của miếng kim loại thứ hai là: 7,8 g/cm3

Crows and foxes
One day, hungry fox to the boil gurgly stomach, it went out of the cave groping in search of food. He saw a pay Crow resting on tree branches high in a cheese closed lips just made. Report crave to tears to pieces, it's a turn rolling his eyes, saw no one around and said to the Crow: "You dear Crow oi, how are you?" The fox Crow glanced just one but did not answer.
Fox tail waved back saying: "My dear Crow You, your voice or how new, how touching, everyone s to hear you sing, you sing a song to go yet."
Fox commended hear crows d the media, a voice exclaimed "but opened his mouth Qua..the cheese falling. Instant quick bite defendants took cheese and fled.
Crows and foxes
One day, hungry fox to the boil gurgly stomach, it went out of the cave groping in search of food. He saw a pay Crow resting on tree branches high in a cheese closed lips just made. Report crave to tears to pieces, it's a turn rolling his eyes, saw no one around and said to the Crow: "You dear Crow oi, how are you?" The fox Crow glanced just one but did not answer.
Fox tail waved back saying: "My dear Crow You, your voice or how new, how touching, everyone s to hear you sing, you sing a song to go yet."
Fox commended hear crows d the media, a voice exclaimed "but opened his mouth Qua..the cheese falling. Instant quick bite defendants took cheese and fled.

Ta có : Đường tròn tâm O cắt O, tại A và B .
=> OO, là đường trung trực của AB .
=> \(\left\{{}\begin{matrix}HA=HB=\frac{1}{2}AB\\AB\perp OO^,\end{matrix}\right.\)
=> \(\widehat{AO^,H}=\frac{1}{2}\widehat{AO^,B}=45^o\)
Mà tam giác AHO, vuông .
=> Tam giác AHO, vuông cân .
- Áp dụng định lý pi ta go vào tam giác AHO, có :
\(AO^,=\sqrt{AH^2+OH^{,2}}=\sqrt{2AH^2}=\sqrt{2\left(\frac{AB}{2}\right)^2}=\sqrt{\frac{AB^2}{2}}\)
- Áp dụng định lý pi ta go vào tam giác AHO, có :
\(O^,H=\sqrt{AO^{,2}-AH^2}=\sqrt{\frac{AB^2}{2}-\left(\frac{AB}{2}\right)^2}=\sqrt{\frac{AB^2}{4}}=\frac{AB}{2}\)
- Áp dụng định lý pi ta go vào tam giác AHO có :
\(OH=\sqrt{AO^2-AH^2}\)
Mà tam giác OAB là tam giác đều ( \(\left\{{}\begin{matrix}OA=OB=R\\\widehat{AOB}=60^o\end{matrix}\right.\) )
=> \(AO=AB\)
=> \(OH=\sqrt{AB^2-\left(\frac{AB}{2}\right)^2}=\sqrt{\frac{3AB^2}{4}}=\frac{AB\sqrt{3}}{2}\)
Ta có : \(OO^,=OH+O^,H=\frac{AB}{2}+\frac{AB\sqrt{3}}{2}=2+2\sqrt{3}\)
=> AB = 4 ( cm )
=> \(AH=BH=\frac{1}{2}AB=2\left(cm\right)\)
- Áp dụng tỉ số lượng giác vào :
\(\left\{{}\begin{matrix}\Delta AHO^,\perp H:SinAO^,H=Sin45=\frac{AH}{AO^,}=\frac{2}{AO^,}\\\Delta AHO\perp H:SinAOH=Sin30=\frac{AH}{AO}=\frac{2}{AO}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}AO^,=2\sqrt{2}=r\\AO=4=R\end{matrix}\right.\) ( cm )

Bài 4:
a: góc C=90-40=50 độ
Xét ΔABC vuông tại A có sin C=AB/BC
nên \(AB=10\cdot sin50=7.66\left(cm\right)\)
=>AC=6.43(cm)
b: Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>AH=DE(1)
Xét ΔBAC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\left(2\right)\)
Từ (1) và (2) suy ra \(DE^2=HB\cdot HC\)
c: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)


Phải có hình dạng thì người ta mới biết OA, OO', góc AOB là những chỗ nào để tính chứ bạn