Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a﴿ Chu vi:
2/5 x 4 = 8/5 ﴾m﴿
Diện tích:
2/5 x 2/5 = 4/25 ﴾m2 ﴿
b﴿ Diện tích 1 ô vuông nhỏ là:
2/25 x 2/25 = 4/625 ﴾m2 ﴿
Số ô vuông cắt được là:
4/25 : 4/625 = 25 ﴾ô vuông﴿
c﴿ Chiều rộng tờ giấy hình chữ nhật là:
4/25 : 4/5 = 1/5 ﴾m﴿

đừng có hỏi các bạn ở đây bằng những câu hỏi hàng tuần ở Online Math bạn ạ,đó là gian lận đấy



Ta có Pt d2 :x+2y-5=0
vì M ϵ d1 :x-y-1=0 nên M(m,m-1)
MA2 = (-1-m)2 + (2-m+1)2 = 1+2m+m2 +9-6m+m2 =2m2 -4m+10
<=> MA=\(\sqrt{2m^2-4m+10}\)
d(m,d2 )= \(\frac{\left|m+2m-2-5\right|}{\sqrt{1^2+2^2}}\) =\(\frac{\left|3m-7\right|}{\sqrt{5}}\)
theo bài ra thì MA=d(M,d2)
=>\(\frac{\left|3m-7\right|}{\sqrt{5}}\)=\(\sqrt{2m^2-4m+10}\) <=>|3m-7|=\(\sqrt{5}\)\(\sqrt{2m^2-4m+10}\)
<=>9m2 -42m +49=5(2m2-4m+10)
<=>9m2 -42m +49=10m2 -20m +50
<=>m2 +22m +1=0
<=>m= -11+2\(\sqrt{30}\) hoặc m=-11-2\(\sqrt{30}\)
=> M(-11+2\(\sqrt{30}\) ,-12+2\(\sqrt{30}\) ) hoặc M(-11-2\(\sqrt{30}\) ,-12-2\(\sqrt{30}\) )

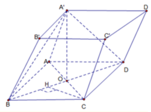
Đáp án C
Do A B ' ∩ A ' B cắt nhau tại trung điểm mỗi đường.
Do đó d B ' = d A = d C
+) Dựng C H ⊥ B D ⇒ C H ⊥ A ' B D
+) Do đó: d B ' ; A ' B D = d C ; A ' B D = C H
= B C . C D B D = a 3 2 .


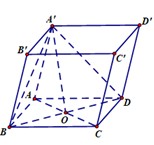

Đáp án A.
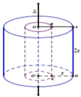
Ta có r 1 = O B = A O − A B = a − x
là bán kính đáy của khối trụ nhỏ.
Và r 2 = O A = a là bán kính đáy của
khối trụ lớn với chiều cao h = 2x
Suy ra thể tích cần tính là
V = V t l − V t n = π r 2 2 h − π r 1 2 h = 2 π x a 2 − a − x 2 = 2 π x 2 a x − x 2 ⇒ V = 2 π x 2 2 a − x = 8 π . x 2 . x 2 . 2 a − x ≤ 8 π . 8 a 3 27 = 64 π a 3 27 ⇒ V max = 64 π a 3 27 .