Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Gọi độ dài ban đầu của các cạnh góc vuông lần lượt là: a; b ( a, b> 0; cm)
=> Diện tích của tam giác vuông ba đầu: \(\frac{1}{2}.a.b\)
Khi tăng mỗi cạnh 2 cm thì diện tích tăng 17 cm ^2
=> \(\frac{1}{2}\left(a+2\right)\left(b+2\right)=\frac{1}{2}.ab+17\)
<=> \(ab+2b+2a+4=ab+34\)
<=> \(a+b=15\)(1)
Khi giảm chiều dài cạnh kia 3cm và cạnh kia 1 cm thì diện tích giảm 11 cm^2
=> \(\frac{1}{2}\left(a-3\right)\left(b-1\right)=\frac{1}{2}ab-11\)
<=> \(ab-3b-a+3=ab-22\)
<=> \(-a-3b=-25\)(2)
Từ (1); (2) => a = 10; b = 5 ( thỏa mãn)
Vậy độ dài hai cạnh cần tìm là 10cm và 5 cm.
Câu 2.
+) Gọi tuổi An hiện nay là x ( x>0; tuổi )
Khi đó tuổi cha An là: 3x (tuổi )
+) 5 năm trước
tuổi An là x - 5 ( tuổi )
tuổi cha An là : 3x - 5 ( tuổi )
Theo bài ra ta có phương trình :
3x - 5 = 4 ( x - 5)
<=> x = 15 ( tm)
Tuổi cha An là : 3 . 15 = 45 tuổi .
Cha An sinh An năm: 45 - 15 = 30 ( tuổi )

\(S_1=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinB\)
\(S_2=\dfrac{1}{2}\cdot3\cdot BC\cdot\dfrac{1}{2}\cdot AB\cdot sinC=\dfrac{3}{4}\cdot BC\cdot AB\cdot sinC\)
=>\(\dfrac{S_2}{S_1}=\dfrac{3}{4}:\dfrac{1}{2}=\dfrac{3}{2}\)
=>Diện tích mới tạo thành bằng 3/2 lần diện tích cũ

Coi cạnh hình vuông ; diện tích hình vuông ban đầu là 100%
Sau khi tăng, cạnh hình vuông chiếm số % là :
100% + 50% = 150%
Sau khi tăng, diện tích hình vuông chiếm số % là:
150% x 150% = 225%
Diện tích hình vuông tăng số % là:
225% - 100% = 125%
50%=1/2
Gọi diện tích hình vuông là b
Cạnh hình vuông mới sẽ là:a+1/2a=3/2a
Diện tích hình vuông mới là:3/2a*3/2a=3/2*3/2*a*a=9/4*b
Diện tích tăng thêm là :9/4b-b=5/4b=125%b
Vậy diện tích tăng thêm là 125%

Chọn D.
Diện tích tam giác ABC ban đầu là
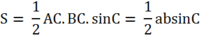
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là
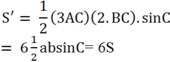

Đặt cạnh huyền của tam giác là x (\(x > 8\))
Theo giải thiết ta tính được cạnh góc vuông là \(x - 8\)
Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} - {{\left( {x - 8} \right)}^2}} = \sqrt {16x - 64} \)
Ta có chu vi của tam giác là \(x + \left( {x - 8} \right) + \sqrt {16x - 64} = 30\)
\(\begin{array}{l} \Leftrightarrow \sqrt {16x - 64} = 38 - 2x\\ \Rightarrow 16x - 64 = {\left( {38 - 2x} \right)^2}\\ \Rightarrow 16x - 64 = 1444 - 152x + 4{x^2}\\ \Rightarrow 4{x^2} - 168x + 1508 = 0\end{array}\)
\( \Rightarrow x = 13\) và \(x = 29\)
Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x - 64} = 38 - 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình
Vậy cạnh huyền có độ dài là 13 cm.

Tính diện tích mảnh bìa hình tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 16,5 dm và 62 cm