Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số góc là:
\(w=\frac{720.2\pi}{60}=25\pi\)
Suất điện động cực đại là:
\(\Rightarrow E_0=N.B.S.w=200\frac{25.10^{-3}}{\pi}.4=500V\)
Suất điện động hiệu dụng là:
\(E=\frac{E_0}{\sqrt{2}}=250\sqrt{2V}\)

\(f=\dfrac{n.p}{60}=\dfrac{3.1200}{60}=60\left(Hz\right)\)
=> C

Nhiệt lượng
\(Q=I^2Rt=\frac{E^2_0t}{2R}=\frac{\left(\omega NBS\right)^2t}{2R}=\frac{\left(200.100\pi.0,002\right)^2.60}{2.1000}\)\(=474J\)

U=E=2πnNBS/60\(\sqrt{2}\)
I=\(\frac{U}{Z}\)=\(\frac{E}{\sqrt{R^2+Z^2_L}}\)

Ta có:
\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R\)
\(4P=\dfrac{U_{2}^{2}}{Z_{2}^{2}}R\)
\(\Rightarrow \dfrac{P}{4P}=\left( \dfrac{U_{1}}{U_{2}} \right)^{2}\left( \dfrac{Z_{2}}{Z_{1}} \right)^{2}\)
\(\Leftrightarrow \dfrac{1}{4}=\left(\dfrac{n_{1}}{n_{2}} \right)^{2}\left(\dfrac{Z_{2}}{Z_{1}} \right)^{2}\rightarrow Z_{2}=Z_{1}\)
Ta nghĩ đến bài toán f biến thiên có 2 giá trị của f mạch cho cùng 1 tổng trở.\(\Rightarrow n_{0}=\sqrt{n_{1}n_{2}}=\sqrt{2}n \)
Vậy khi roto quay với tốc độ \(\sqrt{2}n\) mạch xảy ra cộng hưởng.
Công suất: \(P_0=\dfrac{U_{0}^{2}}{R}\)
Lại có:
\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R=\dfrac{U_{1}^{2}}{2R^{2}}R=\dfrac{U_{1}^{2}}{2R}\) (Do \(Z_1=\sqrt 2.R\))
\(\Rightarrow \dfrac{P}{P_{0}}=\dfrac{U_{1}^{2}}{2U_{0}^{2}}=\dfrac{1}{2}\left(\dfrac{n_{1}}{n_{0}} \right)^{2}=\dfrac{1}{4} \Rightarrow P_{0}=4P\)
Vậy: \(P_0=4P\)
\(U_0=\omega\phi\)
\(P=I^2R=\left(\frac{U_0}{Z\sqrt{2}}\right)^2R=\frac{\omega^2\phi^2R}{2\left(R^2\left(\omega L-\frac{1}{\omega c}\right)^2\right)}\)
\(=\frac{\phi^2R}{2\left(\frac{R^2}{\omega^2}+\left(L-\frac{1}{\omega^2c}\right)^2\right)}=\frac{\phi^2R}{2\left(\frac{1}{\omega^4C^2}+\frac{R^2-2L}{\omega^2}+L^2\right)}\)
Do đó: \(\phi\) không đổi. Đặt : \(\frac{1}{\omega^2}=x\)
Xét f (x) \(=\frac{x^2}{C^2}+\left(R^2-2L\right)x+2L^2\)
=> P_max \(\Leftrightarrow x_0=\frac{2L-R^2}{2C^2}\)
Do P phụ thuộc hàm bậc 2 nên
\(P_1=P_2\Rightarrow x_1+x_2=2x_0\Leftrightarrow\frac{1}{\omega^2_1}+\frac{1}{\omega^2_2}=\frac{2}{\omega^2_0}\)
Mặt khác, tốc độ quay của rôto tỉ lệ thuận với tần số góc nên
\(\frac{1}{n^2_1}+\frac{1}{n^2_2}+\frac{1}{n^2_0}\Leftrightarrow n_0=2\frac{n^2_1n^2_2}{n^2_1+n^2_2}\)

Áp dụng\(\begin{cases}f=np\\E_0=\omega NBS\end{cases}\)\(\Rightarrow\begin{cases}f=np\\E=\omega.k\end{cases}\)(n là số vòng quay của rôto/s, k là hệ số tỉ lệ.
Theo giả thiết ta có:
\(\begin{cases}50=np\\60=\left(n+10\right)p\end{cases}\)\(\Rightarrow\begin{cases}n=50\\p=1\end{cases}\)
\(\begin{cases}E=100\pi k\\E+40=120\pi k\end{cases}\)\(\Rightarrow\pi k=2\)
Nếu tốc độ tăng thêm 60 vòng/phút = 10 vòng/s thì \(n=50+10+10=70\)vòng/s
Tần số: \(f=np=70.1=70\) Hz
Suất điện động hiệu dụng: \(E=140\pi k=140.2=280\)V
Đáp số: \(E=280V\)

Giải thích: Đáp án C
Phương pháp: Công thức tính tần số: f = np (n (vòng/s) là tốc độ quay của roto; p là số cặp cực)
Cách giải:
Ta có: 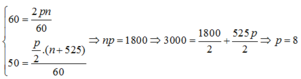
= Số cực từ của máy thứ 2 là: p/2 = 4

C.
n = 300 vòng/giây = 5 vòng/s số cặp cực nam châm p = 10.
Vậy f = np = 50 vòng/giây.

Chọn C
f = n p 60 = n ' p ' 60
⇒ n ' = n p p ' = 600 vòng/ phút