Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(L_1-L_2=10.lg.\left(\frac{h_2}{h_1}\right)^2\Rightarrow h_2=1000\left(m\right)\)
Ta có: \(L_1-L_2=20\log(\dfrac{h_2}{h_1})\)
\(\Rightarrow 120-100=20\log(\dfrac{h_2}{100})\)
\(\Rightarrow h_2=100(m)\)

Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng

Khi mức cường độ âm tăng thêm 10n (dB) thì cường độ âm tăng thêm 10^n lần.
CM:
10lg(I2/I0) - 10lg(I1/I0) = 10n
=> lg(I2/I0) - lg(I1/I0) = n
=> lg(I2/I1) = n
=> I2/I1 = 10^n
=> I2 = 10^n.I1
Vậy khi mức cường độ âm nào đó tăng thêm 30dB thì cường độ của âm tăng lên 1000 lần.
Vậy B đúng
\(L=10log\frac{I}{I_0}\) Khi I tăng 1000 = 103 lần \(\Rightarrow\) L tăng 30 db
chọn B

Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)

+ Tại vị trí ban đầu ta có: L = log P I 0 .4 π .100 2 = 11
+ Để không bị ảnh hưởng tiếng ồn thì khoảng cách mới là R 0 ® L 0 = log P I 0 .4 π . R 0 2 = 9
+ L − L 0 = log R 0 2 100 2 = 2 ® R 0 = 10 2 .100 2 = 1000 m
Vậy cần dịch chuyển khu dân cư ra xa thêm 1 khoảng là d = 1000 − 100 = 900 m.
ü Đáp án C

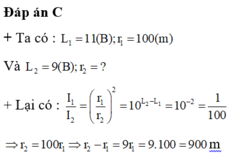
Đáp án: C
HD Giải: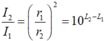
=>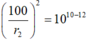
=> r2 = 1000m