Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biểu thức đại số biểu thị chu vi hình chữ nhật là 2(2x+4)

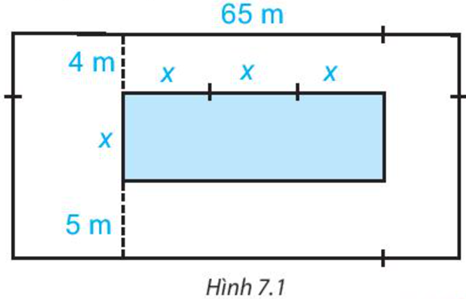
a: Diện tích bể bơi là 3x*x=3x2
b: Diện tích mảnh đất là;
65*(4+x+5)=65(x+9)=65x+585
c: Diện tích phần đất xug quanh là;
65x+585-3x^2
a/Đa thức biểu thị diện tich của bể bơi:
\(A=\) \(3x\cdot x=3x^2\left(m^2\right)\)
b/Chiều rộng mảnh đất:\(4+x+5=x+9\left(m\right)\)
Đa thức biểu thị diện tích mảnh đất:
\(C=65\left(x+9\right)=65x+585\left(m^2\right)\)
c/Đa thức biểu thị diện tích phần đất xung quanh:
\(F=C-A=\left(65x+585\right)-3x^2=-3x^2+65x+585\left(m^2\right)\)

Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(a,b\left(m\right),a>b>0\).
Chu vi là \(30m\)nên \(2\left(a+b\right)=30\Leftrightarrow a+b=15\Leftrightarrow a=15-b\)
Diện tích là \(54m^2\)nên \(ab=54\Leftrightarrow b\left(15-b\right)=54\)
\(\Leftrightarrow\orbr{\begin{cases}b=6\Rightarrow a=9\left(tm\right)\\b=9\Rightarrow a=6\left(l\right)\end{cases}}\)
Tỉ số chiều dài và chiều rộng là: \(\frac{a}{b}=\frac{9}{6}=\frac{3}{2}\).

Gọi chiều rộng, chiều dài của mảnh đất HCN đó lần lượt là: a;b
ta có: -Tỉ số của CR và CD là 5:7
\(\Rightarrow\frac{a}{5}=\frac{b}{7}=k\Rightarrow\hept{\begin{cases}a=5k\\b=7k\end{cases}}\)
- Diện tích HCN là: 140
=> a.b = 140 => 5k.7k = 140
k2 = 4
=>k = 2 hoặc k = -2
k = 2
=> a = 5.2 => a = 10
b = 7.2 => b = 14
k = -2
=> ...
KL:...
Mik giải cách này ko bít có đúng ko
Giả sử chia chiều rộng thành 5 phần bằng nhau thì chiều dài thành 7 phần như thế
Vậy số ô vuông tạo thành là : 5 .7 = 35(ô)
Diện tích mỗi ô vuông là 140 : 35 = 4(m2)
Vậy cạnh hình vuông là : 2m
Chiều rộng mảnh đất là: 2 . 5 = 10 (m)
Chiều dài mảnh đất là: 2 . 7= 14 (m)
Chu vi mảnh vườn là : (10+14) . 2 =48(m)

Gọi cd,cr lần lượt là a,b(m;a,b>0)
Đặt \(\dfrac{a}{3}=\dfrac{b}{2}=k\Rightarrow a=3k;b=2k\)
\(ab=5400\left(m^2\right)\\ \Rightarrow6k^2=5400\\ \Rightarrow k^2=900\\ \Rightarrow k=30\left(k>0\right)\\ \Rightarrow\left\{{}\begin{matrix}a=90\\b=60\end{matrix}\right.\)
Vậy chu vi là \(2\left(a+b\right)=2\cdot150=300\left(m\right)\)
Lời giải:
a.
Chu vi hình chữ nhật: $2(x+y)$ (m)
Diện tích hình chữ nhật: $xy$ (m2)
b.
Chiều rộng: $12-2=10$ (m)
Chu vi: $2(x+y)=2(12+10)=44$ (m)
Diện tích: $12\times 10=120$ (m2)