Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

\(\Leftrightarrow\left(a+1,b+2\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
\(\Leftrightarrow\left(a,b\right)\in\left\{\left(0;1\right);\left(2;-1\right);\left(-2;-5\right);\left(-4;-3\right)\right\}\)

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Ta luôn có \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) và \(\left|x-y\right|=\left|y-x\right|\)
\(\Rightarrow\left|x-2\right|=\left|2-x\right|;\left|x-4\right|=\left|4-x\right|;...;\left|x-8\right|=\left|8-x\right|;\left|x-10\right|=\left|10-x\right|\)
\(\Rightarrow A=\left|x-1\right|+\left|2-x\right|+\left|x+3\right|+\left|4-x\right|+...+\left|x-9\right|+\left|10-x\right|\)
\(\Rightarrow A\ge\left|x-1+2-x+x-3+4-x+...+x-9+10-x\right|\)
\(=\left|\left(x-x+x-x+x-x+...+x-x\right)+\left(2-1\right)+\left(4-3\right)+...+\left(10-9\right)\right|\)
\(=\left|0+1+1+1+1+1\right|\)
\(=5\)
\(\Rightarrow A\ge5\)
\(\Rightarrow\) GTNN của A = 5 tại \(\left(x-1\right)\left(2-x\right)\left(x-3\right)...\left(x-10\right)\ge0\)

để phải làm số hộp hình vuông là ít nhất thì hộp hình lâp phuong có canh là UCLN(16;20;12) = 4
VẬY cạnh hình lập phuong là 4cm
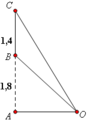
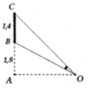

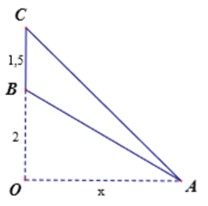
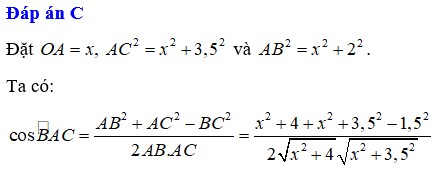
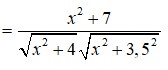


Đáp án A
Phương pháp giải: Dựa vào hệ thức lượng trong tam giác và công thức lượng giác xác định độ lớn của góc cần tính thông qua khoảng cách. Khảo sát hàm số tìm min – max
Lời giải: Với bài toán này, ta cần xác định OA để góc BOC lớn nhất. Điều này xảy ra khi tan BOC lớn nhất.
Đặt OA = x(m) với x > 0. Ta có: