Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=48/2=24dm
AB=AC=căn AH^2+HC^2=26(dm)
Xét ΔAHB có BM/BA=BE/BH=1/2
nên ME//AH và ME=1/2AH=5dm
Xét ΔCAH có CN/CA=CF/CH
nên NF//AH
=>NF/AH=CF/CH=1/2
=>NF=5dm
ΔAHB vuông tại H có HM là trung tuyến
nên HM=AB/2=13dm

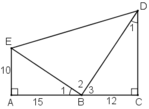
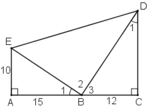
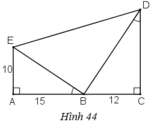
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
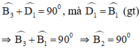
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
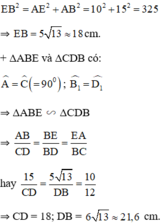
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
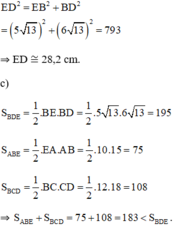

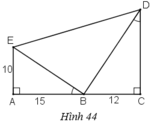
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
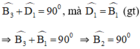
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
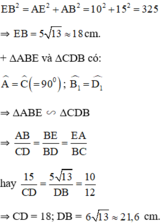
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
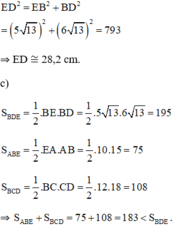

\(7,\)
\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân\right)\\\widehat{B_1}=\widehat{C_1}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\\\widehat{BAC}.chung\end{matrix}\right.\Rightarrow\Delta AFC=\Delta AEB\left(g.c.g\right)\\ \Rightarrow AF=AE\Rightarrow\Delta AFE.cân.tại.A\)
\(b,\left\{{}\begin{matrix}\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân\right)\\BC.chung\\\widehat{B_2}=\widehat{C_2}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\end{matrix}\right.\Rightarrow\Delta BFC=\Delta CEB\left(g.c.g\right)\)
\(c,\widehat{F_1}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta AEF.cân\right);\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta ABC.cân\right)\\ \Rightarrow\widehat{F_1}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị nên \(EF//BC\Rightarrow BEFC\) là hình thang
Mà \(\widehat{ABC}=\widehat{ACB}\left(GT\right)\)
Vậy \(BEFC\) là hình thang cân

a: Thanh nẹp còn lại phải làm có độ dài là:
căn 6^2+8^2=10(m)
b: AC^2=AB^2+BC^2
=>ΔABC vuông tại B
AC^2=AD^2+DC^2
=>ΔACD vuông tại D


ta có △ABC cân → dg cao AH là dg trung tuyến
→ HB = HC = BC/2 = 7,6/2 =3,8cm
ad pitago có AB2 = BH2 + AH2 = 1,52 + 3,82
→ AB = 4,1cm
BCDE là hình thang cân nên ta có
SBCDE = BC*BK + BK*KE = 7,6*2,5 + 2,5*KE
= 19 + 2,5*KE
mà diên tích BCDE có thể tính theo công thức
SBCDE = ( BC + BE) * BK/2 = \(\dfrac{7,6+10}{2}\)* 2,5 = 22cm2
từ (1) và (2) ⇒ 19 +2,5*KE = 22
KE = 1,2cm
ad pitago BE2 = BK2 + KE2 = 2,52 + 1,22
⇒ BE = 2,77cm
tổng chiều dài các thanh sắt sử dụng = AB*2 + BE*2 = 4,1*2 + 2,77*2 =13,74cm