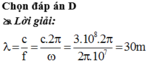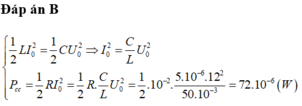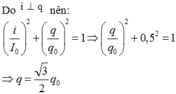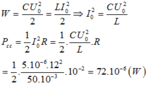Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạch LC có i vuông qua với q nên:
\((\dfrac{i}{I_0})^2+(\dfrac{q}{Q_0})^2=1\)\(\Rightarrow (\dfrac{i}{\omega Q_0})^2+(\dfrac{q}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega Q_0})^2+(\dfrac{q_1}{Q_0})^2=1\)
\((\dfrac{i_2}{\omega Q_0})^2+(\dfrac{q_2}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega })^2+(q_1)^2=(\dfrac{i_2}{\omega })^2+(q_2)^2\)
\(\Rightarrow \omega ^2=\dfrac{i_1^2-i_2^2}{q_2^2-q_1^2}\)
\(\Rightarrow T=\dfrac{2\pi}{\omega}=2\pi.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
\(\Rightarrow \lambda = c.T =2\pi c.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
Chọn B.

Chọn đáp án A
Thời gian ngắn nhất để năng lượng điện trường giảm từ giá trị cực đại (giả sử lúc này q = Q 0 ) xuống còn một nửa giá trị cực đại q = Q 0 2 là T 8 = 1 , 5 . 10 - 4 s , suy ra T = 1 , 2 . 10 - 3 s .
Thời gian ngắn nhất để điện tích trên tụ giảm từ giá trị cực đại xuống còn một nửa giá trị đó là T / 6 = 2 . 10 - 4 s