Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số học sinh thích cả bóng chuyền và bóng rổ là: 23 + 18 – 26 = 15 (học sinh)
Số học sinh thích bóng chuyền và không thích bóng rổ là 23 – 15 = 8 (học sinh)
Vậy xác suất để chọn được học sinh thích bóng chuyền và không thích bóng rổ là \(\frac{8}{{40}} = \frac{1}{5}\)
Đáp án C

Gọi A: “Học sinh thích môn Bóng đá”
B: “Học sinh thích môn Bóng bàn”
Do đó ta có \(P\left( A \right) = \frac{{19}}{{30}},P\left( B \right) = \frac{{17}}{{30}},P\left( {AB} \right) = \frac{{15}}{{30}}\)
Theo công thức cộng xác suất
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{19}}{{30}} + \frac{{17}}{{30}} - \frac{{15}}{{30}} = \frac{{21}}{{30}} = \frac{7}{{10}}\)
Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là \(\frac{7}{{10}}\)

Cặp biến cố E và F không xung khắc vì nếu học sinh được chọn thích môn Bóng đá thì cả E và F có thể xảy ra vì có 2 bạn thích cả hai môn Bóng đá và Cầu lông.
Vì có 2 bạn cùng thích bóng đá và cầu lông
nên hai biến cố E và F không xung khắc

Gọi A là biến cố “Bạn đó thích nhạc cổ điển”, B là biến cố “Bạn đó thích nhạc trẻ”, C là biến cố “Bạn đó không thích cả nhạc cổ điển và nhạc trẻ”.
a) Xác suất bạn đó thích nhạc cổ điển là \(P\left( A \right) = \frac{{14}}{{40}} = \frac{7}{{20}}\)
Xác suất bạn đó thích nhạc trẻ là \(P\left( B \right) = \frac{{13}}{{40}}\)
Xác suất bạn đó thích cả nhạc cổ điển và nhạc trẻ là \(P\left( C \right) = \frac{5}{{40}} = \frac{1}{8}\)
Xác suất bạn đó thích nhạc cổ điển hoặc nhạc trẻ là
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{7}{{20}} + \frac{{13}}{{40}} - \frac{1}{8} = \frac{{11}}{{20}}\)
b) Ta có \(\overline C = A \cup B\) nên xác suất để bạn đó không thích cả nhạc cổ điển và nhạc trẻ là
\(P\left( C \right) = 1 - P\left( {\overline C } \right) = 1 - P\left( {A \cup B} \right) = 1 - \frac{{11}}{{20}} = \frac{9}{{20}}\)

Ta có n(Ω) = 40
c) Nhận thấy :
![]()
![]()
Mà P(A∪B) = P(A) + P(B) –P(A∩B), A∩B là biến cố:”học sinh được chọn giỏi cả Văn và Toán” nên n(A∩B)=5/40=1/8
![]()
![]()
Chọn đáp án C
Nhận xét:
ở ý a) và b) học sinh có thể nhầm khi quan niệm: chọn 1 học sinh nên n(A) =n(B) =1 ⇒ phương án A; hoặc chọn 1 học sinh trong 5 học sinh giỏi Toán và Văn nên n(A) =n(B) = 5
⇒ P(A) =P(B) =5/40=1/8 (phương án D); hoặc sử dụng nhầm công thức P(A) =(n(Ω))/(n(A))=8/3;P(B)=(n(Ω))/(n(B))=4 (phương án C)
ở ý c), học sinh có thể nhầm khi quan niệm:
![]()
![]()
![]()
Nhưng A ¯ v à B ¯ không phải là hai biến cố độc lập

![]()
Có thể giải ý c) cách khác như sau:
Số học sinh giỏi Văn và Toán gồm: học sinh giỏi Văn, học sinh hioir Toán, học sinh giỏi cả Văn và Toán nên bằng (15 +10) -5 = 20 em. Do đó, số học sinh không giỏi cả Toán và Văn là 40 – 20 = 20 em, nên n(C) = 20
Vì vậy P(C) =(n(C))/(n(Ω))=1/2

Ta có n(Ω) = 40
a) Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8
Chọn đáp án là C

Ta có n(Ω) = 40
b) Rõ ràng n(B) = 10 nên P(B) = 10/40 =1/4
Chọn đáp án B

Gọi B là tập hợp “học sinh thích học Lý”
Gọi C là tập hợp ” học sinh thích học ít nhất một môn “
Ta có n(C) = n( A ∪ B) = n(A) + n(B) – n(A ∩ B) = 30 + 25 – 10 = 45
Vậy xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý là: 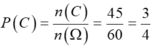
Chọn B.

Lời giải:
a. Xác suất chọn hsg là:
$\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}=\frac{17}{50}$
b.
Chọn ngẫu nhiên 3 hs, có $C^3_{100}$ cách chọn
Số hsg là: $(\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}).100=34$ (hs)
Chọn ngẫu nhiên được 2 hsg có $C^2_{34}C^1_{100-34}=C^2_{34}.C^1_{66}$ cách chọn
Xác suất cần tìm: $p=\frac{C^2_{34}.C^1_{66}}{C^3_{100}}=\frac{561}{2450}$
Số học sinh thích cả bóng chuyền và bóng rổ là: 23 + 18 – 26 = 15 (học sinh)
Gọi A là biến cố “Học sinh thích bóng chuyền”; B là biến cố “Học sinh thích bóng rổ”; E là biến cố “Học sinh không thích cả bóng chuyền và bóng rổ”.
Khi đó \(\overline E \) là biến cố “Học sinh thích bóng chuyền hoặc bóng rổ”.
Ta có \(\overline E = A \cup B.\)
\(P\left( A \right) = \frac{{23}}{{40}},P\left( B \right) = \frac{{18}}{{40}} = \frac{9}{{20}},P\left( {AB} \right) = \frac{{15}}{{40}} = \frac{3}{8}\)
\(\begin{array}{l}P\left( {\overline E } \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{23}}{{40}} + \frac{9}{{20}} - \frac{3}{8} = \frac{{13}}{{20}}\\ \Rightarrow P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - \frac{{13}}{{20}} = \frac{7}{{20}}\end{array}\)
Vậy xác suất để chọn được học sinh không thích cả bóng chuyền và bóng rổ là \(\frac{7}{{20}}\).
Đáp án B.