Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích một mặt bên của lồng đèn là: \(10.30 = 300\left( {c{m^2}} \right)\)
Tổng diện tích các mặt bên của chiếc lồng đèn đó là: \(300.6 = 1800\left( {c{m^2}} \right)\)

Kẻ SG vuông góc (ABC)
S.ABC là khối chóp đều
=>ΔABC đều
=>G là trọng tâm, là trực tâm của ΔABC
Gọi giao của AG với BC là D
=>D là trung điểm của BC
ΔABC đều có AD là trung tuyến
nên \(AD=\dfrac{a\sqrt{3}}{2}\)
=>\(AG=\dfrac{a\sqrt{3}}{2}\cdot\dfrac{2}{3}=\dfrac{a\sqrt{3}}{3}\)
ΔSAG vuông tại G nên \(SG=\sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{1}{3}a^2}\)
\(V_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SG=\dfrac{1}{3}\cdot\sqrt{b^2-\dfrac{1}{3}a^2}\cdot\dfrac{a^2\sqrt{3}}{4}\)
\(=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{\dfrac{3b^2-a^2}{3}}\)
Thể tích khối tứ diện đều có cạnh bằng a là:
\(V=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a^3\sqrt{2}}{12}\)

Đáp án A
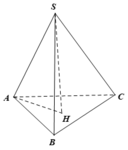
Gọi H là tâm của tam giác đều ABC => SH ⊥ (ABC)
(SA;(ABC))![]()
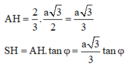
![]()
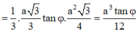
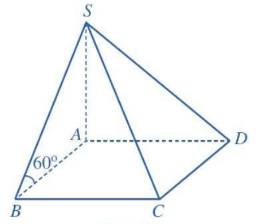
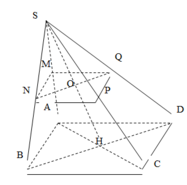
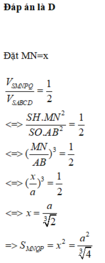
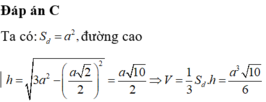



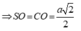
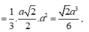
Mô hình hoá đèn đá muối bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\).
Gọi \(O\) là tâm của đáy.
\(\Delta SAC\) cân tại \(S\) \( \Rightarrow SO \bot AC\)
\(\Delta SBD\) cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\\{V_{S.ABC{\rm{D}}}} = \frac{1}{3}.{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\end{array}\)