Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Gọi số cần tìm là \(\overline{abc}\). Vậy nếu chuyển số cuối lên đầu, ta được số mới có dạng \(\overline{cba}\)
Theo đề bài ra ta có: \(\overline{cab}=5.\overline{abc}+25\)
Vì \(\overline{cab}\) và \(\overline{abc}\) đều là số có 3 chữ số, nên a chỉ có thể là 1. Vì nếu a = 2 thì tích \(5.\overline{abc}\) có giá trị lớn hơn 1000
b = 0 hoặc b = 5 vì \(5.\overline{abc}+25\) sẽ có chữ số tận cùng là 0 hoặc 5
- TH1: b = 0
Ta có: \(\overline{c10}=5.\overline{10c}+25\)
\(\overline{c00}+10=500+c+25\)
99c = 515
c = \(\frac{515}{99}\) ( loại )
- TH2: b = 5
Ta có: \(\overline{c15}=5.\overline{15c}+25\)
\(\overline{c00}+15=750+5c+25\)
95c = 760
=> c = 8 ( thoả mãn )
Vậy số có 3 chữ số cần tìm là 158

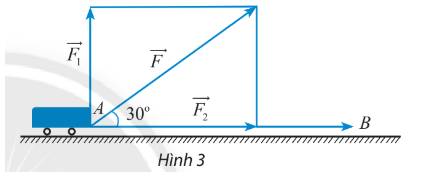
Ta xác định được các độ lớn:
\(\left| {\overrightarrow F } \right| = 50,\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow F } \right|\cos 30^\circ = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 ,\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right|.\sin 30^\circ = 50.\frac{1}{2} = 25\) (N)
Dựa vào hình vẽ ta có: \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 30^\circ ,\left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 90^\circ ,\left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 0^\circ \)
Áp dụng công thức tính công sinh ra bởi lực \(A = \overrightarrow F .\overrightarrow d \) ta có:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 50.200.\cos 30^\circ = 5000 (J)\)
\({A_1} = \overrightarrow {{F_1}} .\overrightarrow d = \left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 25.200.\cos 90^\circ = 0 (J)\)
\({A_2} = \overrightarrow {{F_2}} .\overrightarrow d = \left| {\overrightarrow {{F_2}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 25\sqrt 3 .200.\cos 0^\circ = 5000\sqrt 3 (J)\)

Theo giải thiết ta có tam thức sau: \(f\left( x \right) = 20.15 - \left( {20 + x} \right)\left( {15 - x} \right) = {x^2} + 5x\)
Tam thức có \(\Delta = 25 > 0\), có hai nghiệm phân biệt \({x_1} = 0;{x_2} = -5\)
Vậy khoảng diện tích tăng lên là \(x>0\) và \(x<-5\), khoảng diện giảm đi là \(x \in(-5;0)\) và diện tích không đổi khi \(x = 0\) và \(x = -5\)

nếu tăng chiều dài thêm 15cm và giữ nguyên chiều rộng thì diện tích tăng thêm 150cm² thì chiều rộng của hình chữ nhật đó là:
150:15=10(cm)
chiều dài hình chữ nhật đó là:
10x3=30(cm)
diện tích ban đầu của hình chữ nhật đó là:
10x30=300(cm²)