Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một lăng trụ đứng, đáy là một tam giác thì lăng trụ đó có 5 mặt, 9 cạnh, 6 đỉnh.
Vậy chọn đáp án B

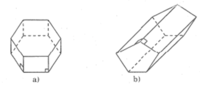
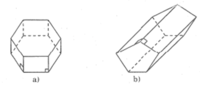
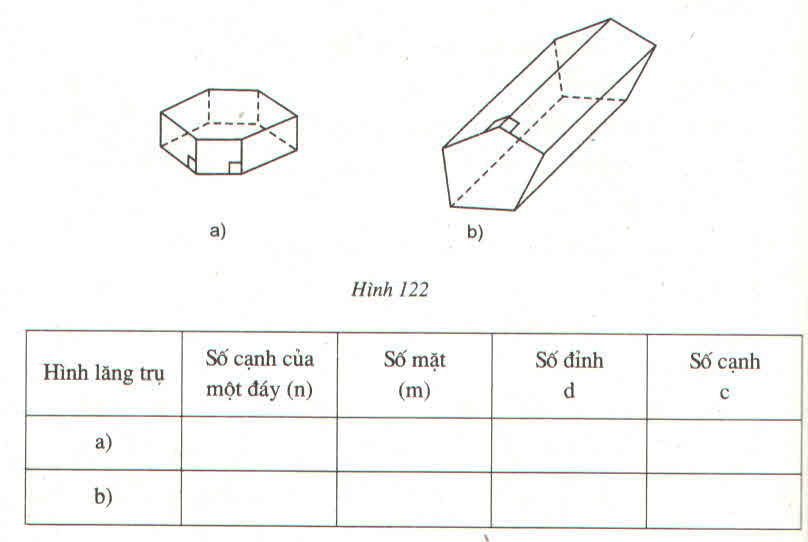
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)

| Hình lăng trụ | SỐ cạnh của một đáy | Số mặt | SỐ đỉnh | SỐ cạnh |
| a | 6 | 8 | 12 | 18 |
| b | 5 | 7 | 10 | 15 |
a: m=n+2
d=2n;
c=3n
b: Số cạnh của một đáy là:
n=d/2=20/2=10(cạnh)
c: Hình lăng trụ có 20 đỉnh thì
Số mặt là m=n+2=10+2=12(mặt)
Số cạnh là c=3n=30(cạnh)
d: Không thể làm một hình lăng trụ có 15 đỉnh bởi 15 là số lẻ

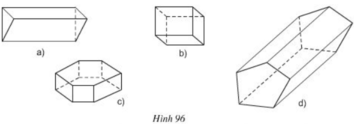
| Hình | a | b | c | d |
| Số cạnh của một đáy | 3 | 4 | 6 | 5 |
| Số mặt bên | 3 | 4 | 6 | 5 |
| Số đỉnh | 6 | 8 | 12 | 10 |
| Số cạnh bên | 3 | 4 | 6 | 5 |

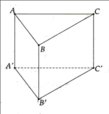
a) Ta có:
- Các đỉnh: A, B, C, A', B' và C'
- Các cạnh bên: AA', BB' và CC'.
- Các cạnh đáy: AB, BC, CA, A'B', B'C' và C'A'.
- Các mặt đáy: ABC và A'B'C'
- Các mặt bên: ABB'A', BCC'B' và CAA'C'
b) AB và CC' chéo nhau, AC và A'B' chéo nhau. Các mặt phẳng (ABB'A') và (BCC'B') cắt nhau theo giao tuyến BB'.
Chọn B