Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có:
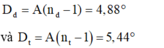
- Góc lệch của 2 tia đỏ và tím là:
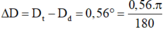
→ Khoảng cách từ vệt đỏ đến tím là:
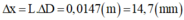

Đáp án A
Góc lệch của tia đỏ và tia tím qua lăng kính:

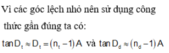
Vậy độ rộng quang phổ là:

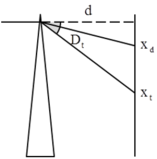
I H D T D
Góc lệch của tia sáng khi qua lăng kính: \(D=(n-1)A\)
Suy ra: \(D_đ=(n_đ-1)A\)
\(D_t=(n_t-1)A\)
Bề rộng quang phổ trên màn: \(DT=HT-HD=IH.\tan D_t -IH.\tan D_đ\)
Khi góc \(\alpha \) rất nhỏ thì \(\tan\alpha\approx\alpha_{rad}\)
\(\Rightarrow DT=IH( D_t -D_đ)=IH.(n_t-n_đ).A\)
\(\Rightarrow DT = 1.(1,68-1,61).\dfrac{8}{180}\pi=0,0122m=1,22cm\)

Chọn C.
Độ rộng quang phổ trên màn là ĐT = AE(nt – nđ)A = 0,97cm.

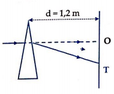
(xem Hình 24.1G)
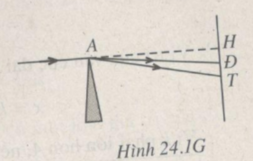
Gọi A là góc chiết quang của lăng kính ;
H là giao điểm của đường kéo dài của tia tới với màn ảnh ; Đ và T là vết của tia đỏ và tia tím trên màn ảnh. Góc lệch của tia đỏ và tia tím là
D đ = A( n đ -1)
D t = A( n t - 1)
Khoảng cách từ các vết đỏ và vết tím đến điểm H là :
HĐ = AH.tan D đ = AH.tanA( n đ - 1)
HT = AH.tan D t = AH.tanA( n t - 1)
Độ rộng từ màu đỏ đến màu tím của quang phổ liên tục trên màn ảnh là :
ĐT = HT - HĐ = AH[tanA( n t - 1) - tanA( n đ - 1)] với A = 6 ° ; n t - 1,685 ; n đ = 1,642 ; AH = 1,2 m thì ĐT = 5,4 mm.

Chọn đáp án A.
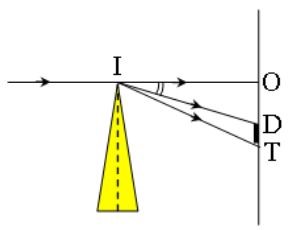
n d sin A = sin i d ⇒ 1 , 532 sin 30 0 = sin i d ⇒ i d ≈ 50 0 ⇒ D d = i d − A = 20 0 n t sin A = sin i t ⇒ 1 , 5867 sin 30 0 = sin i t ⇒ i t ≈ 52 , 5 0 ⇒ D t = i t − A = 22 , 5 0
D T = I O ( tan D t − tan D d ) = 1000 ( tan 22 , 5 0 − tan 20 0 ) ≈ 50 ( m m ) .
Chú ý: Nếu lăng kính có góc chiết quang bé và góc tới bé thì D = ( n − 1 ) A ⇒ D d = ( n d − 1 ) A D t = ( n t − 1 ) A
⇒ δ = D t − D d = ( n t − n d ) A
Độ rộng quang phổ lúc này: D T = I O ( tan D t − tan D d ) ≈ I O ( D t − D d ) = I O ( n t − n d ) A

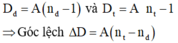
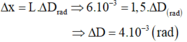
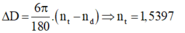
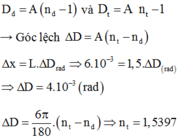
Chọn đáp án D