Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài ta có dãy số chỉ số ghế có ở các hàng là một cấp số cộng có số hạng đầu \({u_1} = 17\) và công sai \(d = 3\).
a) Số ghế có ở hàng cuối cùng là: \({u_{20}} = {u_1} + 19{\rm{d}} = 17 + 19.3 = 74\) (ghế).
b) Tổng số ghế có trong rạp là: \({S_{20}} = \frac{{20\left[ {2{u_1} + 19{\rm{d}}} \right]}}{2} = \frac{{20\left[ {2.17 + 19.3} \right]}}{2} = 910\) (ghế).

Cấp số cộng có u10 = 380; d = 30
⇒u1=u10−9d=110
Số ghế trong hội trường:
\(S_{10}=\dfrac{10\left(110+380\right)}{2}=2450\)

Đáp án C
Xét 2 khả năng:
+) Trường hợp ở giữa có 3 ghế có thể xếp nam ở bên phải hoặc trái nên số cách xếp
là 2.4!.2!=96
+) Trường hợp ở giữa có 2 ghế thì ghế ngoài cùng bên phải hoặc bên trái sẽ trống.
Tương ứng số cách sắp xếp là 2.2.4!.2!=192
Vậy số cách sắp xếp là 192 + 96 = 288

Đáp án C
Xét 2 khả năng:
+) Trường hợp ở giữa có 3 ghế có thể xếp nam ở bên phải hoặc trái nên số cách xếp là
2.4!.2!=96
+) Trường hợp ở giữa có 2 ghế thì ghế ngoài cùng bên phải hoặc bên trái sẽ trống
Tương ứng số cách sắp xếp là 2.2.4!.2!=192
Vậy số cách sắp xếp là 192 + 96 = 288

· Gọi nhóm I là nhóm ghế của 4 bạn nam, số cách xếp là 4!, tương tự với 2 bạn nữ là nhóm II với số cách xếp là 2!.
· Rõ ràng khi xếp 6 bạn này vào hàng 9 ghế thì ta còn 3 ghế trống. Chia 9 hàng ghế này thành 5 phần có thứ tự, trong đó 2 phần bất kì nào dành cho nhóm I và nhóm II thì 3 phần còn lại sẽ là 3 chiếc ghế trống.
· Số cách xếp 2 nhóm vào 9 hàng ghế sao cho nam ngồi liền nhau, nữ ngồi liền nhau là: Coi nhóm I, nhóm II và 1 ghế trống ở giữa 2 nhóm này là 1 nhóm đại diện, số nhóm đại diện là 2!. Lúc này 9 ghế hàng ngang thì còn lại 2 ghế trống. Tương tự chia 9 hàng ghế làm 3 phần với ý tưởng khi nhóm đại diện rơi vào 1 phần nào đó thì 2 phần còn lại sẽ là ghế trống, khi đó số cách xếp nam ngồi liền nhau, nữ ngồi liền nhau và giữa 2 nhóm có đúng 1 ghế trống là: ![]()
Vậy số cách xếp cần tìm là: ![]()
chọn B.

Bước 1: Ta sử dụng tính chất riêng của hai bạn B và F trước. Hai bạn này chỉ ngồi đầu và ngồi cuối, hoán đổi cho nhau nên có 2! cách xếp.
Bước 2: Xếp vị trí cho các bạn còn lại, ta có cách xếp.
Vậy ta có 2!.5! = 240 cách xếp
Chọn C.

Chọn B
Xếp 9 người vào 9 ghế kê hàng ngang ta có: Ω =9! cách sắp xếp.
Gọi B là biến cố để “mỗi thầy giáo ngồi giữa 2 học sinh và học sinh A ngồi ở một trong hai đầu hàng.”
Theo đề, học sinh A ngồi ở một trong hai đầu hàng nên có 2 cách sắp xếp.
Xếp 5 học sinh còn lại vào 5 vị trí có 5! cách sắp xếp. Xem mỗi học sinh tạo thành một vách ngăn tạo thành 5 khoảng trống. Xếp 3 thầy vào 5 khoảng trống có A 5 3 cách.
![]() cách.
cách.
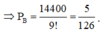

Chọn C
Cách 1: Mỗi cách xếp thỏa mãn yêu cầu bài toán chính là một chỉnh hợp chập 3 của 5 phần tử nên số cách xếp là A 5 3 (cách).
Cách 2: Có 5 cách xếp bạn A, với mỗi cách xếp bạn A thì có 4 cách xếp bạn B, với mỗi cách xếp bạn A và B thì có 3 cách xếp bạn C. Vậy theo qui tắc nhân có 5.4.3 = 60(cách).

Đáp án A
Phương pháp :
+) Chọn vị trí cho các bạn nam (hoặc nữ).
+) Hoán đổi các vị trí.
+) Sử dụng quy tắc nhân.
Cách giải : Chọn 1 vị trí trong 2 vị trí đối xứng có C 2 1 cách chọn, như vậy có ( C 2 1 ) 4 = 2 4 cách chọn ghế cho 4 bạn nam.
4 bạn nam này có thể đổi chỗ cho nhau nên có 4! cách xếp
Vậy có 4!4!24 cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ.


Ta có: \({u_1} = 15,\;d = 3\)
\({S_n} = \frac{n}{2}\left[ {2 \times 15 + \left( {n - 1} \right) \times 3} \right] = 870\)
\(\frac{n}{2}\left( {27 + 3n} \right) = 870\)
\(\begin{array}{l} \Leftrightarrow 3{n^2} + 27n - 1740 = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 20\\n = - 29(L)\end{array} \right.\end{array}\)
Vậy cần phải thiết kế 20 hàng ghế.