Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Lấy lần 1 và lần 2 đã lấy ra được 1 sản phẩm loại I và 1 sản phẩm loại II, do đó còn $15$ sản phẩm loại I và $3$ sản phẩm loại II (tổng 18 sản phẩm)
Trong lần thứ 3:
Lấy ngẫu nhiên 1 sản phẩm, có $C^1_18=18$ cách chọn
Lấy ngẫu nhiên 1 sản phẩm loại II từ 3 sản phẩm loại II, có $C^1_3=3$ cách chọn
Xác suất để lấy được sản phẩm loại II: $\frac{3}{18}=\frac{1}{6}$

\(n\left(\Omega\right)=C^4_{10}=210\)
A: "Không chọn được hai chiếc nào tạo thành một đôi".
\(\overline{A}\): "Chọn được ít nhất hai chiếc tạo thành một đôi".
\(n\left(\overline{A}\right)=C^1_5\cdot C_8^2=140\).
\(n\left(A\right)=210-140=70\).
\(P\left(A\right)=\dfrac{70}{210}=\dfrac{1}{3}\).

a: n(omega)=4+3+3+5=15
n(xanh)=4+3=7
=>P=7/15
b: P=7/15*4/7=4/15

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 chiếc giày trong số 8 chiếc giày.
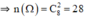
A: “ Chọn được 2 chiếc tạo thành một đôi”
⇒ n(A) = 4 (Vì có 4 đôi).
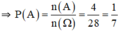

Phép thử T được xét là: "Lấy ngẫu nhiên 2 chiếc giày từ 4 đôi giày có cỡ khác nhau".
Mỗi một kết quả có thể là một tổ hợp chập 2 của 8 chiếc giày. Do đó số các kết quả có thể có thể có của phép thử T là n(Ω) = C28 = = 28.
Vì lấy ngẫu nhiên, nên các kết quả có thể có của phép thử T là đồng khả năng. Gọi A là biến cố: "Lấy được hai chiếc giày tạo thành một đôi". Mỗi một kết quả có thể có thuận lợi cho A là một đôi giày trong 4 đôi giày đã cho. Do đó số các kết quả có thể có thuận lợi cho A là n(A) = 4. Suy ra P(A) = =
.

Gọi K là biến cố "Có ít nhất một động cơ chạy tốt",khi đó biến cố đối của K là biến cố D. Do đó
P(K)=1-P(D)=0,94.
Chọn D.

Đáp án C
Phương pháp: Tính số phần tử của không gian mẫu và số phần tử của biến cố, sau đó suy ra xác suất.
Cách giải: Ba lần quay, mỗi lần chiếc kim có 7 khả năng dừng lại, do đó n Ω = 7 3 = 243
Gọi A là biến cố: “trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau" Khi đó ta có:
Lần quay thứ nhất, chiếc kim có 7 khả năng dừng lại.
Lần quay thứ hai, chiếc kim có 6 khả năng dừng lại.
Lần quay thứ ba, chiếc kim có 5 khả năng dừng lại.
Do đó nA = 7.6.5 = 210
Vậy
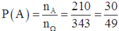

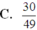
Lời giải:
2 lần chọn đầu có 1 chiếc tốt và 1 chiếc lỗi, tức là còn 15 chiếc tốt là 3 chiếc lỗi
Xác suất để chọn lần thứ ba được chiếc ti vi bị lỗi là:
$p=\frac{C^1_3}{C^1_{18}}=\frac{3}{18}=\frac{1}{6}$
dạ em cám ơn Thầy ạ