Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Không thể chắc chắn bạn Sơn rút được phiếu câu hỏi số 2
b) Có 20 kết quả xảy ra

Không chắc chắn bạn Sơn rút được phiếu câu hỏi mình mong muốn.

Gọi \(A\) là biến cố người được chọn ngẫu nhiên ủng hộ việc tắt điện trong sự kiện Giờ Trái Đất.
Xác suất thực nghiệm của biến cố \(A\) là \(\frac{{255}}{{300}} = 0,85\).
Do số người chọn lớn nên \(P\left( A \right) \approx 0,85\).
Vậy xác suất của biến cố “Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ việc tắt đèn điện trong sự kiện Giờ Trái Đất” khoảng 0,85.

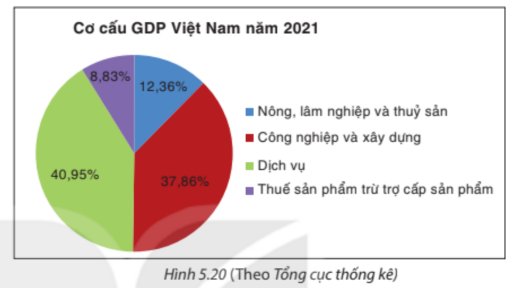
a) Lĩnh vực đóng góp nhiều nhất vào GDP là dịch vụ, với 40,95%
b) Lĩnh vực dịch vụ đóng góp: 400 x 40,95% = 163,8 (tỉ đô la Mỹ)

Gọi x là số chỗ ngồi của mỗi xe bé ( x > 0 )
=> Số chỗ ngồi của mỗi xe lớn = x + 15
Dùng loại xe lớn => Số xe = 180/x+15
Dùng loại xe bé => Số xe = 180/x
Nếu dùng loại xe lớn thì phải dùng ít hơn loại xe nhỏ 2 chiếc
=> Ta có phương trình : \(\frac{180}{x}-\frac{180}{x+15}=2\)
<=> \(\frac{180\left(x+15\right)}{x\left(x+15\right)}-\frac{180x}{x\left(x+15\right)}=\frac{2x\left(x+15\right)}{x\left(x+15\right)}\)
<=> \(180x+2700-180x=2x^2+30x\)
<=> \(2700=2x^2+30x\)
<=> \(x=\orbr{\begin{cases}30\\-45\end{cases}}\)
Vì x > 0 => x = 30
=> Số xe lớn được huy động là \(\frac{180}{30+15}=4\)xe
Giải lại phương trình để cho bạn hiểu :
\(\frac{180}{x}-\frac{180}{x+15}=2\) ( đkxđ : x \(\ne\)0 ; x \(\ne\)15 )
<=> \(\frac{180\left(x+15\right)}{x\left(x+15\right)}-\frac{180x}{x\left(x+15\right)}=\frac{2x\left(x+15\right)}{x\left(x+15\right)}\)
<=> \(180x+2700-180x=2x^2+30x\)
<=> \(2x^2+30x=2700\)
<=> \(2x^2+30x-2700=0\)
<=> \(2\left(x-30\right)\left(x+45\right)=0\)
<=> \(\orbr{\begin{cases}x-30=0\\x+45=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=30\\x=-45\end{cases}}\)

Theo đề bài ta có sơ đồ
Người 2 i-------i-------i
Người 1 i-------i-------i--------i
Biết người 1 + người 2 = 5 (Phần)
Công việc được hoàn thành trong 12 ngày
=> 5*12=60 ( Phần )
Theo đề bài ta có được: + Người thứ 1 sẽ làm số ngày là 60/3 = 20 ( ngày )
+ Người thứ 2 sẽ làm số ngày là 60/2= 30 ( ngày )

gọi X là công việc
X/15-((X/2)/15+(X/2)/18)=20/60
=>X=60 sản phẩm
1111111111111111111111111111111111111111111111111111111111111111111111111111111
Vì gặp ngẫu nhiên một người trong 200 người nên 200 kết quả có khả năng xảy ra như nhau.
Số người làm Kinh doanh trong 200 người ở khu phố là:
\(200.24\% = 48\) (người)
Số người làm Y tế trong 200 người ở khu phố là:
\(200.12\% = 24\) (người)
Số người làm Giáo dục trong 200 người ở khu phố là:
\(200.10\% = 20\) (người)
Số người làm Sản xuất trong 200 người ở khu phố là:
\(200.30\% = 60\) (người)
Số người làm Dịch vụ trong 200 người ở khu phố là:
\(200.24\% = 48\) (người)
a) Gọi \(A\) là biến cố người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục.
Biến cố \(A\) xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục do đó, số kết quả thuận lợi của biến cố \(A\) là 20. Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{{20}}{{200}} = \frac{1}{{10}}\)
b) Gọi \(B\) là biến cố người gặp ngẫu nhiên không thuộc lĩnh vực Y tế hay Dịch vụ do đó, người gặp ngẫu nhiên có thể thuộc lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất.
Biến cố \(B\) xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất do đó, số kết quả thuận lợi của biến cố \(B\) là: 48 + 20 + 60 = 128.
Xác suất của biến cố \(B\) là:
\(P\left( B \right) = \frac{{128}}{{200}} = \frac{{16}}{{25}}\).