Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ![]()
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có ![]()
X: “lấy được 2 bi viên xanh” ta có: ![]()
V: “lấy được 2 bi viên vàng” ta có: ![]()
T: “ lấy được 2 bi màu trắng” ta có : ![]()
Ta có D; X; V; T là các biến cố đôi một xung khắc và A= D ∪ X ∪ V ∪ T
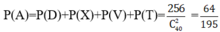
Chọn B.

Ta có, số phần tử của không gian mẫu n ( Ω ) = C 10 2
Gọi các biến cố: D: “lấy được 2 viên đỏ” ; X: “lấy được 2 viên xanh” ;
V: “lấy được 2 viên vàng”
Ta có D, X, V là các biến cố đôi một xung khắc và C = D ∪ X ∪ V
P ( C ) = P ( D ) + P ( X ) + P ( V ) = C 4 2 C 10 2 + C 3 2 C 10 2 + C 2 2 C 10 2 = 2 9
Chọn đáp án B

Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là: ![]()
Suy ra:n(A)=4095.
Chọn C.

Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là:![]()
Suy ra : ![]()
Chọn C.

Chọn A
Lời giải
Không gian mẫu là số sách chọn ngẫu nhiên mỗi hộp 1 viên bi
Số phần tử của không gian mẫu là Ω = C 15 1 . C 18 1
Gọi X là biến cố "2 viên bi lấy ra từ mỗi hộp có cùng màu"
Ta có các kết quả thuận lợi cho biến cố X như sau
● Hộp A lấy ra 1 bi trắng và hộp B lấy ra 1 bi trắng, có C 4 1 . C 7 1 cách
● Hộp A lấy ra 1 bi đỏ và hộp B lấy ra 1 bi đỏ, có C 5 1 . C 6 1 cách
● Hộp A lấy ra 1 bi xanh và hộp B lấy ra 1 bi xanh, có C 6 1 . C 5 1 cách
Suy ra số phần tử của biến cố
![]()
Vậy xác suất cần tính
P ( X ) = Ω x Ω = 44 135

Không gian mẫu: \(C_{15}^4\)
a.
Số cách lấy 4 viên bi trong đó có 3 viên màu đỏ: \(C_7^3C_8^1\)
Xác suất: \(P=\dfrac{C_7^3.C_8^1}{C_{15}^4}\)
b.
Lấy 4 viên không có viên đỏ nào (lấy từ 8 viên 2 màu còn lại): \(C_8^4\) cách
Lấy 4 viên có ít nhất 1 viên đỏ: \(C_{15}^4-C_8^4\)
Xác suất: \(P=\dfrac{C_{15}^4-C_8^4}{C_{15}^4}\)
c.
Các trường hợp thỏa mãn: (2 đỏ 1 xanh 1 vàng), (1 đỏ 2 xanh 1 vàng), (1 đỏ 1 vàng 2 xanh)
Số cách lấy: \(C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2\)
Xác suất: \(P=\dfrac{C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2}{C_{15}^4}\)

Trong bình có tổng cộng \(5+6+7=18\) viên bi
Không gian mẫu: \(n_{\Omega}=C_{18}^4=3060\)
a. Gọi A là biến cố "trong 4 viên bi được chọn có đúng 1 viên đỏ"
Chọn 1 viên bi đỏ từ 5 viên đỏ: \(C_5^1\) cách
Chọn 3 viên còn lại từ 13 viên (6 trắng 7 vàng): \(C_{13}^3\) cách
\(\Rightarrow n_A=C_5^1.C_{13}^3=1430\)
Xác suất: \(P=\dfrac{1430}{3060}=...\)
b. Gọi B là biến cố "4 viên được chọn có ít nhất 2 viên vàng"
Chọn 4 viên có đúng 1 viên vàng (1 viên vàng và 3 viên từ 2 loại khác): \(C_7^1.C_{11}^3=1155\) cách
Chọn 4 viên không có viên vàng nào: \(C_{11}^4=330\) cách
Xác suất: \(P_B=1-\dfrac{1155+330}{3060}=...\)

a) Không gian mẫu : \(\left|\Omega\right|=C^3_{18}=816\)
Biến cố A" 3 bi cùng màu"
Các trường hợp thuận lợi cho biến cố A "
TH1: 3 bi trắng \(C^3_8\)
TH2: 3 bi vàng \(C^3_6\)
TH3: 3 bi xanh \(C^3_4\)
=> \(\left|\Omega_A\right|=C^3_8+C^3_6+C^3_4=80\)
=> \(P\left(A\right)=\dfrac{80}{816}=\dfrac{5}{51}\)
b) Biến cố B" 3 bi khác màu"
Chọn mỗi màu 1 viên
Màu trắng 8 cách
Màu vàng 6 cách
Màu xanh 4 cách
=> \(\left|\Omega_B\right|=8\cdot6\cdot4=192\)
=> \(P\left(B\right)=\dfrac{\left|\Omega_B\right|}{\left|\Omega\right|}=\dfrac{192}{816}=\dfrac{4}{17}\)
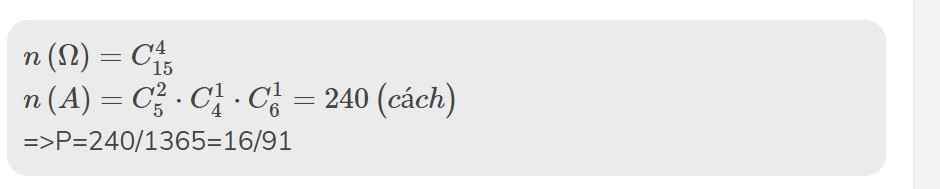
Ta có: số phần tử của không gian mẫu là Ω = C 40 2
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có: n D = C 20 2 = 190 ;
X: “lấy được 2 bi viên xanh” ta có: n X = C 10 2 = 45 ;
V: “lấy được 2 bi viên vàng” ta có: n V = C 6 2 = 15 ;
T: “ lấy được 2 bi màu trắng” ta có: n T = C 4 2 = 6 .
Ta có D,X,V,T là các biến cố đôi một xung khắc và A = D ∪ X ∪ V ∪ T
Suy ra xác xuất để lấy được 2 viên bi cùng màu là:
P A = P D + P X + P V + P T = 256 C 40 2 = 64 195 .
Chọn đáp án D.