Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Yêu cầu bài toán thỏa mãn khi ta rút được 3 thẻ sao cho trong đó không có 2 thẻ nào là số tự nhiên liên tiếp
Số cách rút được 3 thẻ bất kì là C 26 3
Số cách rút được 3 thẻ có đúng 2 số tự nhiên liên tiếp:
Chọn 2 số tự nhiên liên tiếp: {1;2}{2;3}…{25;26}
TH1: Chọn 2 thẻ là {1;2} hoặc{25;26}: có 2 cách
Thẻ còn lại không được là 3 (hoặc 24): 26 -3 =23 (cách)
→ 2.23 =46 (cách)
TH2: Chọn 2 thẻ là: {2;3},{3;3},…{24;25}: 23 cách
Thẻ còn lại chỉ có: 26 -4 =22 (cách) →có 23.22 =506 (cách)
Số cách rút 3 thẻ trong đó có 3 số tự nhiên liên tiếp:
{1;2;3}{2;3;4}…{24;25;26}: 24 cách
Vậy có: C 26 3 - 46 - 506 - 24 = 2024 .
Chọn đáp án D.

Chọn B.
Số cách rút hai thẻ chẵn là C 10 2 . Số cách rút ra hai thẻ trong đó có một thẻ ghi số chia hết cho 4 còn thẻ kia ghi số lẻ là .
Vậy xác suất cần tìm là C 5 1 C 5 2
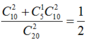

Chọn đáp án C
Cách 1: Gọi P n A là xác suất rút ít nhất được một thẻ ghi số chia hết cho 4 từ n lần rút.
Gọi P n B là xác suất không rút được thẻ ghi số chia hết cho 4 từ n lần rút.


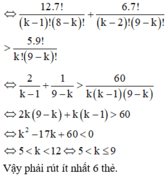

HD: Số phần tử của không gian mẫu là: Ω = C 11 4
Gọi A là biến cố: “Tổng số ghi trên 4 tấm thẻ ấy là một số lẻ”
Khi đó số tấm lẻ được chọn là số lẻ.
Trong 11 số từ 1 đến 11 có 6 số lẻ và 5 số chẵn.


Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra P = 60 + 100 C 11 4 = 16 33

Chọn C.
Số phần tử của không gian mẫu là: n Ω = C 11 6 = 462
Gọi A là biến cố “ Chọn ngẫu nhiên 6 tấm thẻ để tổng ghi trên 6 tấm thẻ là một số lẻ”
Các kết quả thuận lợi cho biến cố A.
Lấy ra được 1 tấm thẻ lẻ và 5 tấm thẻ chẵn có C 6 1 . C 5 5
Lấy ra được 3 tấm thẻ lẻ và 3 tấm thẻ chẵn có C 6 3 . C 5 3
Lấy ra được 5 tấm thẻ lẻ và 1 tấm thẻ chẵn có C 6 5 . C 5 1
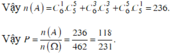



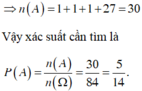

Đáp án D