Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Gọi T là biến cố "Trong 4 quả lấy ra có 3 quả cầu trắng".
\(\left|\Omega\right|=C^4_{15}\)
\(\left|\Omega_T\right|=C^3_7.C^1_8\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^3_7.C^1_8}{C^4_{15}}=\dfrac{8}{39}\)

Không gian mẫu: \(C_{10}^3\)
a. Xác suất: \(\dfrac{C_4^2.C_6^1}{C_{10}^3}=...\)
b. \(P=\dfrac{C_4^2C_6^1+C_4^3}{C_{10}^3}=...\)
c. \(P=\dfrac{C_6^3}{C_{10}^3}=...\)

Không gian mẫu là kết quả việc chọn ngẫu nhiên 4 quả cầu từ hộp 10 quả cầu.
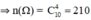
a. A: “ Bốn quả lấy ra cùng màu”
TH1: Bốn quả lấy ra cùng đen
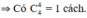
TH2: Bốn quả lấy ra cùng trắng
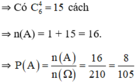
b. B: “ Cả 4 quả lấy ra đều màu đen”
⇒ B−: “ Có ít nhất 1 quả màu trắng”.
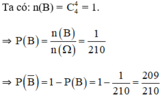

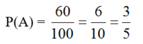
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai
+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;
⇒ n(Ω) = 10.10 = 100.
A: “ Quả cầu lấy từ hộp thứ nhất trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B
⇒ n(A) = 6.10 = 60.
B: “Quả cầu lấy từ hộp thứ hai trắng”
⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A
⇒ n(B) = 4.10 = 40.
A.B: “Cả hai quả cầu lấy ra đều trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B
⇒ n(A.B) = 6.4 = 24.
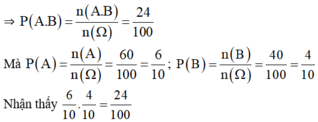
hay P(A.B) = P(A).P(B)
⇒ A và B là biến cố độc lập.
b) Gọi C: “Hai quả cầu lấy ra cùng màu”.
Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”
B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”
⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”
Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)
Và C=(A.B)∪(A−.B−)
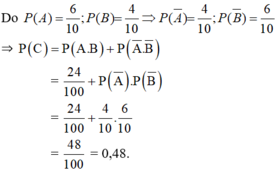
c) C− : “Hai quả cầu lấy ra khác màu”
⇒ P(C− )=1-P(C)=1-0,48=0,52

- Số cách lấy ngẫu nhiên 2 quả cầu: \(n\left( \Omega \right) = C_9^2 = 36\)
- Số cách lấy 2 quả khác màu là:
+ 1 quả màu xanh và 1 quả màu vàng: \(C_4^1 \times C_3^1 = 12\)
+ 1 quả màu xanh và 1 quả màu đỏ: \(C_4^1 \times C_2^1 = 8\)
+ 1 quả màu đỏ và 1 quả màu vàng: \(C_2^1 \times C_3^1 = 6\)
=> Tổng số cách lấy ra 2 quả khác màu là: 26 cách
- Số cách lấy 2 quả khác màu trùng số:
+ 2 quả cùng là số 1: \(C_3^2 = 3\)
+ 2 quả cùng là số 2: \(C_3^2 = 3\)
+ 2 quả cùng là số 3: \(C_2^2 = 1\)
=> Tổng số cách lấy ra 2 quả khác màu trùng số là: 7 cách
=> Số cách lấy ra 2 quả khác màu khác số là: 26 – 7 = 19 (cách)
=> Xác suất để lấy ra 2 quả khác màu khác số là: \(P = \frac{{19}}{{36}}\)

Số cách chọn hai quả cầu cùng màu là:
\(5\cdot4+3\cdot2=26\left(cách\right)\)
Số quả cầu tất cả là 5+3=8(quả)
Xác suất để chọn hai quả cầu cùng màu là:
\(\dfrac{26}{8\cdot7}=\dfrac{13}{28}\)

Đáp án D
Lấy ngẫu nhiên 2 quả cầu trong 5 quả cầu có
C 5 2 cách
Suy ra số phần tử của không gian mẫu là
![]()
Gọi X là biến cố “lấy được cả hai quả cầu trắng”
Lấy 2 quả cầu trắng trong 3 quả cầu trắng có C 3 2 cách
⇒ n ( X ) = C 3 2 = 3
Vậy xác suất cần tính là