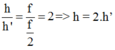Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Cơ năng của vật:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot0,5\cdot4^2+0,5\cdot10\cdot5=29J\)
b)Cơ năng tại nơi có độ cao cực đại: \(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow29=mgh_{max}\Rightarrow h_{max}=\dfrac{29}{0,5\cdot10}=5,8m\)
c)Cơ năng tại nơi động năng bằng thế năng:
\(W_2=W_đ+W_t=2W_t=2mgh'\left(J\right)\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow29=2mgh'\Rightarrow h'=\dfrac{29}{2\cdot0,5\cdot10}=2,9m\)

ta giải từng câu theo phương pháp bảo toàn cơ năng (bỏ ma sát), lấy g = 10 m/s², gốc thế năng tại mặt đất.
Dữ kiện: ban đầu vật ở cao \(h_{0} = 30\) m, vận tốc ban đầu hướng lên \(v_{0} = 20\) m/s.
Tổng cơ năng (trên mỗi đơn vị khối lượng \(m\) nếu muốn) là
\(E = g h_{0} + \frac{1}{2} v_{0}^{2} = 10 \cdot 30 + \frac{1}{2} \cdot 20^{2} = 300 + 200 = 500 \left(\right. \text{m}^{2} / \text{s}^{2} \left.\right) .\)
a) Độ cao lớn nhất so với mặt đất
Tại điểm cao nhất vận tốc \(v = 0\). Dùng bảo toàn năng lượng:
ghmax=E⇒hmax=Eg=50010=50 m.gh_{\max} = E \quad\Rightarrow\quad h_{\max}=\frac{E}{g}=\frac{500}{10}=50\ \text{m}.ghmax=E⇒hmax=gE=10500=50 m.
Đáp án (a): \(50 \&\text{nbsp};\text{m} .\)
b) Tìm độ cao mà ở đó động năng bằng thế năng
Gọi \(h\) là độ cao cần tìm. Động năng trên mỗi đơn vị khối lượng là \(\frac{1}{2} v^{2}\), thế năng là \(g h\). Bảo toàn năng lượng cho ta \(\frac{1}{2} v^{2} = E - g h\). Yêu cầu \(\frac{1}{2} v^{2} = g h\) nên
\(E - g h = g h \textrm{ }\textrm{ } \Rightarrow \textrm{ }\textrm{ } E = 2 g h \textrm{ }\textrm{ } \Rightarrow \textrm{ }\textrm{ } h = \frac{E}{2 g} = \frac{500}{20} = 25 \&\text{nbsp};\text{m} .\)
Lưu ý: vật ban đầu ở 30 m, nên lúc ban đầu động năng < thế năng; vật sẽ đi lên đến 50 m rồi rơi xuống, và khi rơi đến \(h = 25\) m thì động năng bằng thế năng.
Đáp án (b): \(25 \&\text{nbsp};\text{m} .\)
(Thêm: tốc độ tại đó có thể tính: \(\frac{1}{2} v^{2} = g h = 10 \cdot 25 = 250 \Rightarrow v^{2} = 500 \Rightarrow v = \sqrt{500} \approx 22,36 \&\text{nbsp};\text{m}/\text{s} .\))
c) Tìm tốc độ ở vị trí mà động năng bằng ba lần thế năng
Yêu cầu: \(\frac{1}{2} v^{2} = 3 g h\). Từ bảo toàn năng lượng: \(\frac{1}{2} v^{2} = E - g h\). Do đó
\(E - g h = 3 g h \textrm{ }\textrm{ } \Rightarrow \textrm{ }\textrm{ } E = 4 g h \textrm{ }\textrm{ } \Rightarrow \textrm{ }\textrm{ } h = \frac{E}{4 g} = \frac{500}{40} = 12,5 \&\text{nbsp};\text{m} .\)
Khi đó \(\frac{1}{2} v^{2} = 3 g h = 3 \cdot 10 \cdot 12,5 = 375\). Vậy
\(v^{2} = 750 \Rightarrow v = \sqrt{750} \approx 27,39 \&\text{nbsp};\text{m}/\text{s} .\)
Đáp án (c): tốc độ \(v = \sqrt{750} \approx 27,39 \&\text{nbsp};\text{m}/\text{s}\) (độ lớn của vận tốc; chiều có thể lên hoặc xuống tuỳ lúc vật đi qua vị trí đó).

Công mà lớp nước rộng 1km2, dày 1m, có độ cao 200m có thể sinh ra khi chảy vào tuabin là: A = Ph = Vdh (V là thể tích, d là trọng lượng riêng của nước).
A = (1000000.1). 10000.200 = 2.1012J.
Công đó bằng thế năng của lớp nước, khi vào tuabin sẽ dược chuyển hóa thành điện năng.
→ Đáp án B

Công mà lớp nước rộng 1km2, dày 1m, có độ cao 200m có thể sinh ra khi chảy vào tuabin là:
A = P.h = 10.m.h = 10. V.D.h = 10. S.d.D.h
(V là thể tích, D là khối lượng riêng của nước, d là bề dày lớp nước).
→ A = 10.106.1.1000.200 = 2.1012J.
Công đó bằng thế năng của lớp nước, khi vào tuabin sẽ được chuyển hóa thành điện năng.

Ta có:
Lượng năng lượng điện tối đa thu được bằng công của lượng nước rơi xuống:
W=A=P.h
Lại có:
P=10m=10.DV
V= S d
Ta suy ra: W=10.D.V.h=10.D.S.d.h
Từ đề bài ta có:
S = 1 k m 2 = 10 6 m 2
d=1m
D=1000kg/ m 3
h=200m
→W=10.1000. 10 6 .1.200= 2 . 10 12 J
Đáp án: B

Công mà lớp nước dày 1m, rộng 1km2 và độ cao 200m có thể sinh ra khi chảy vào tuabin là : A = P.h = V.d.h = 1000000 . 1 . 10000. 200 = 2.1012J.
(V là thể tích khối nước, d là trọng lượng riêng của nước)
Công đó bằng thế năng của lớp nước, khi vào tuabin sẽ được chuyển hóa thành điện năng.