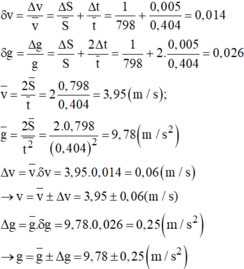Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức tính sai số tỉ đối
δv = =
+
=
+
= 0,014
δg = =
+
=
+2.
= 0,026
=
= 2.
= 3,95 m/s
∆v = .δv = 3,95 . 0,014 = 0,06 m/s
v = ± ∆v = 3,95 ± 0,06 m/s
mà =
=
= 9,78 m/s2.
∆g = .δg = 9,78.0,026 = 0,26 m/s2.
g = ± ∆g = 9,78 ± 0,26 m/s2

\(g=\overline{g}\pm\Delta g=9,78\pm0,44\)
Sai số tỉ đối:
\(\delta g=\dfrac{\Delta g}{\overline{g}}\cdot100\%=\dfrac{0,44}{9,78}\cdot100\%\approx4,5\%\)

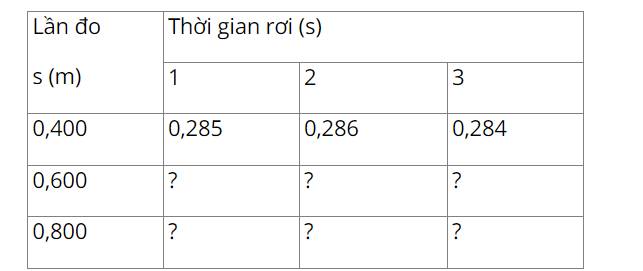
Để tính kết quả của phép đo thời gian rơi tự do của vật, ta cần lấy trung bình của các kết quả đo và trừ đi sai số của đồng hồ đo.
Trung bình của các kết quả đo là: (0,404 + 0,406 + 0,403) / 3 = 0,4043 s.
Sai số của đồng hồ đo là 0,001 s.
Vậy, kết quả của phép đo thời gian rơi tự do của vật được ghi là 0,4043 - 0,001 = 0,4033 s.

Câu 1.
Thời gian vật rơi trên cả quãng đường:
\(S=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot80}{10}}=4s\)
Vận tốc vật khi chạm đất:
\(v=g\cdot t=10\cdot4=40\)m/s
Chọn B.

Ta có
g=\(\dfrac{G.M}{r^2}\)=9,8
=>G.M=9,8.r2
gh=\(\dfrac{G.M}{(r+h)^2}\)=\(\dfrac{9,8.r^2}{(r+r/2)^2}\)=9,8r2:(3/2 .r)2=9,8r2:(9/4.r2)=4,3(5)m/s2
g1=\(\dfrac{G.M}{\left[r+h\right]^2}\)=\(\dfrac{G.M}{\left[2h+h\right]^2}\)=\(\dfrac{G.M}{\left[r+\dfrac{1}{2}r\right]^2}\)=\(\dfrac{G.M}{\left[\dfrac{3}{2}r\right]^2}\)
g2=\(\dfrac{G.M}{r^2}\)
=>\(\dfrac{g_1}{g_2}\)=\(\dfrac{r^2}{\dfrac{9}{4}r^2}\) <=>\(\dfrac{9,8}{g_2}\)=\(\dfrac{9}{4}\)
<=>g2=9,8/\(\dfrac{9}{4}\) \(\simeq\)4,36 m/s2