Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
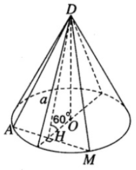
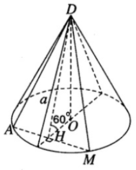
Xét mặt phẳng (DAM) đi qua đỉnh D tạo với mặt phẳng đáy một góc 600, cắt đường tròn đáy tại hai điểm A và M. Từ tâm O của đường tròn đáy ta vẽ OH ⊥ AM, do vậy H là trung điểm của đoạn AM. Ta có AM ⊥ (DOH) vì AM ⊥ OH và AM ⊥ DO.
Vậy
∠
DHO = 60
°
và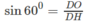 
hay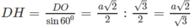 
Gọi SΔ DAM là diện tích thiết diện cần tìm, ta có: S △ DAM = AH.DH
Mà 
Vậy
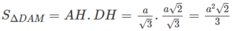
a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)
Thiết diện qua trục của hình nón là tam giác vuông cân cạnh a nên hình nón có đường sinh l = a,
có bán kính đáy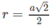 
và có chiều cao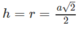 
Gọi S xq là diện tích xung quanh của hình nón, ta có:
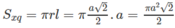
Gọi S là diện tích đáy của hình nón, ta có
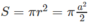
Vậy diện tích toàn phần của hình nón đã cho là:
Hình nón có thể tích là:
