Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(\left\{{}\begin{matrix}\text{%A+%G=50%N}\\\%A-\%G=10\%\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\%A=\%T=30\%N\\\%G=\%X=20\%N\end{matrix}\right.\)
Vì gen chứa 3600 liên kết hidro:
H=3600
<=> 2A+3G=3600
<=>2.30%N+3.20%N=3600
<=>N=3000(Nu)
Chiều dài của gen:
L=N/2 x 3,4= 3000/2 x 3,4=5100(Ao)
b) Số nu từng loại của gen:
A=T=30%N=30%.3000=900(Nu)
G=X=20%N=20%.3000=600(Nu)

Theo đè bài ra ta có HPT: \(\left\{{}\begin{matrix}G-A=10\%\\A+G=50\%\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}A=T=20\%\\G=X=30\%\end{matrix}\right.\)
a) Số lk H của gen là:
20%N.2 + 30%N.3= 3900
<=>N=3000
a) Số lượng từng loại nu của gen là:
G=X=3000.30%=900(nu)
A=T=3000.20%=600(nu)
b)Số lượng nu khi ở kì giữa ngphan là:
G=X=900.2=1800(nu)
A=T=600.2=1200(nu)

1,theo NTBS, ta co tong cua 2 loai Nu khong bo sung nhau luon bang nhau va bang 50% tong so Nu cua toan phan tu.Theo đề bài ,tổng của 2 loại Nu bằng 90%chỉ có thể là tổng của 2 loại Nu bổ sung cho nhau
TH1:Nếu A+T=90%=>A=T=90%/2=45%;G=X=50%-45%=5%
TH2:Nếu G+X=90%=.G=X=90%/2=45%=>A=T=50%-45%=5%
2,-then NTBS,ta coG=X=>X-G=0
-theo đề baihieu giữa Nu loại G với 1 Nụ loại khác =30%nên chỉ có thể là hiệu giữa G với A hay T
-ta co: G-A=20%(1)
Theo NTBS;G+A=50%(2)
lay (1)+(2),=>2G=70%=>G=X=35%; A=T=50%-35%=15%
3, goi 2 loai Nu khong bo sung cho nhau la A va G
-theo đề bài , tả cô:A xG=6%=0.06 (1)
A+G=50%=0,5(2)
tu (1) va (2) =.A va G la nghiem cua phuong trinh:x2-0,5x+0,06=0
giai phuong trinh ta tim duoc x1=0,3;x2=0,2
có 2 trường hợp:A=T=30%;G=X=20% hoặc A=T=20%;G=X=30%

a.
N = 5100 . 2 : 3,4 = 3000 nu
2A + 3G = 3600
2A + 2G = 3000
-> A = T = 900 nu, G = X = 600 nu
b.
rU - rA = 120
rU + rA = 900
-> rU = 510 nu, rA = 390 nu
rG / rX = 2/3
rG + rX = 600
-> rG = 240 nu, rX = 360 nu
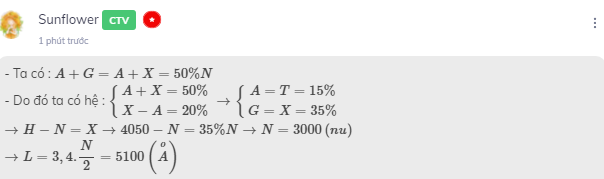
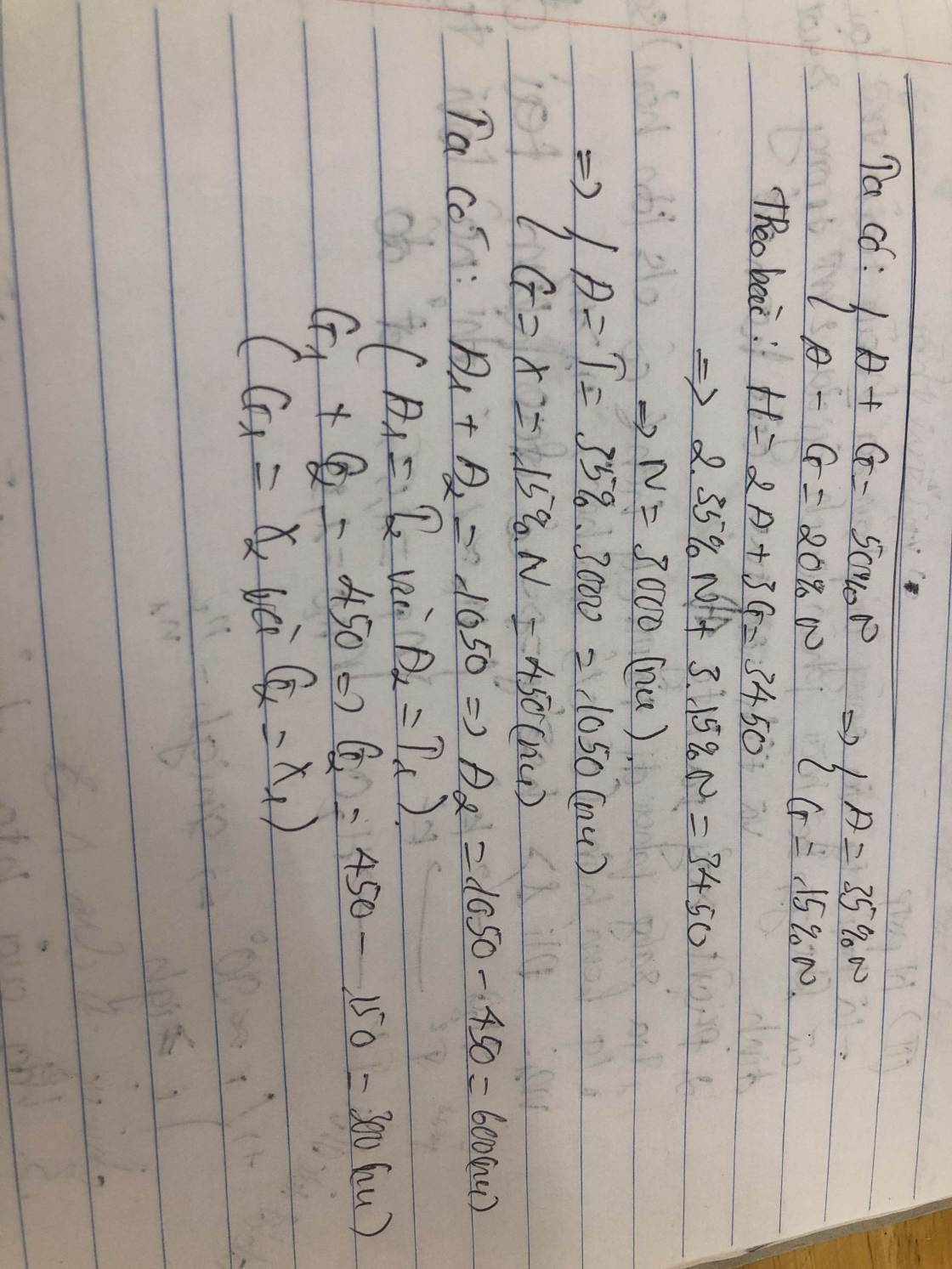
+, Trường hợp 1:
Ta có: \(\left\{{}\begin{matrix}X-A=140\\2A+3X=2520\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}X=G=560\\A=T=420\end{matrix}\right.\)
+, Trường hợp 2:
Ta có: \(\left\{{}\begin{matrix}A-X=140\\2A+3X=2520\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}X=G=448\\A=T=588\end{matrix}\right.\)