Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

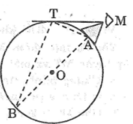
Điểm nhìn tối đa T là tiếp điểm của tiếp tuyến kẻ từ mắt đến bề mặt Trái Đất (như hình vẽ)
Xét hai tam giác MTA và MBT,ta có:
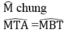
(hệ quả góc giữa tiếp tuyến và dây cung)
Suy ra ∆ MTA đồng dạng ∆ MBT
⇒ MT/MA = MB/MT => M T 2 = MA.MB
= MA (MA + 2R)
MA là chiều cao của đỉnh núi bằng 1km
Thay số ta có: M T 2 =1.(1 + 2.6400)=12801
Suy ra : MT ≈ 113,1(km)


Áp dụng kết quả bài 34 ta có:
+ MT2 = MA.MB
MA = 40m = 0,04km ;
MB = MA + AB = MA + 2R = 12800,04 km.
⇒ MT ≈ 22,63 km
+ M’T2 = M’A’.M’B’
M’A’ = 10m = 0,01km ;
M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km
⇒ M’T ≈ 11,31 km
⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .
Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

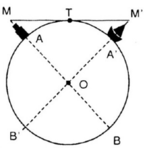
Áp dụng kết quả bài 34 ta có:
+ M T 2 = M A . M B
MA = 40m = 0,04km ;
MB = MA + AB = MA + 2R = 12800,04 km.
⇒ MT ≈ 22,63 km
+ M ’ T 2 = M ’ A ’ . M ’ B ’
M’A’ = 10m = 0,01km ;
M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km
⇒ M’T ≈ 11,31 km
⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .
Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

Phương pháp giải
Sử dụng: Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân tan góc đối.

Đặt tên như hình vẽ thì chiều cao của tháp là đoạn BDBD
Xét tam giác ABCABC vuông tại AA có AC=DE=150m;ˆC=200AC=DE=150m;C^=200 nên
AB=150.tan20∘≈54,596(m)AB=150.tan20∘≈54,596(m)
Chiều cao của cột ăng-ten là:
BD=AB+ADBD=AB+AD=54,596+1,5=56,096(m).

Khoảng cách tối đa là \(\sqrt{3049.\left(3049+6400000.2\right)}\approx197577\left(m\right)\)