Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi C = C1 hoặc C = C2 thì I như nhau, do vậy:
\(Z_1=Z_2\Rightarrow Z_L-Z_{C1}=Z_{C2}-Z_L\Rightarrow Z_L=\dfrac{Z_{C1}+Z_{C2}}{2}=45\Omega\)
Để cường độ hiệu dụng qua R cực đại thì mạch xảy ra cộng hưởng.
\(\Rightarrow Z_C=Z_L=45\Omega\)
Chọn A.

Điện áp ko đổi nhưng vẫn có dòng điện và dòng điện hữu hạn, chứng tỏ chỉ có 2 trường hợp:
1. Điện trở và cuộn cảm mắc nối tiếp (nối tiếp với tụ thì sẽ ko thể có dòng chạy qua)
2. Điện trở song song với tụ điện (nếu song song với cuộn cảm thuần thì sẽ bị chập mạch, tức là dòng lớn vô cùng)
Có thể bỏ qua trường hợp này vì điều kiện thứ 2.
Xét trường hợp 1:
Dễ dàng tính được: \(R=\frac{30}{2.5}=12\Omega\)
Mắc nối tiếp hộp kín với tụ điện C, ta có mạch RLC nối tiếp.
Theo bài ra, ta có hình vẽ: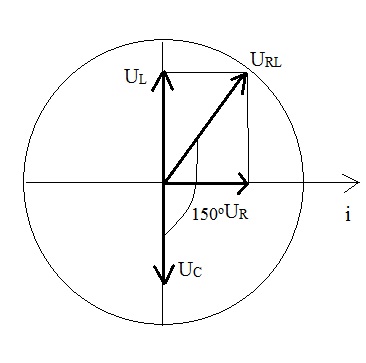
Từ hình vẽ ta có:
\(U_R=U_L\tan30^o\)
Suy ra:
\(Z_L=\frac{R}{\tan30^o}=12\sqrt{3}\Omega\)
Tổng trở của hộp kín:
\(Z=\sqrt{R^2+Z^2_L}=24\Omega\)

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Mạch LC có i vuông qua với q nên:
\((\dfrac{i}{I_0})^2+(\dfrac{q}{Q_0})^2=1\)\(\Rightarrow (\dfrac{i}{\omega Q_0})^2+(\dfrac{q}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega Q_0})^2+(\dfrac{q_1}{Q_0})^2=1\)
\((\dfrac{i_2}{\omega Q_0})^2+(\dfrac{q_2}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega })^2+(q_1)^2=(\dfrac{i_2}{\omega })^2+(q_2)^2\)
\(\Rightarrow \omega ^2=\dfrac{i_1^2-i_2^2}{q_2^2-q_1^2}\)
\(\Rightarrow T=\dfrac{2\pi}{\omega}=2\pi.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
\(\Rightarrow \lambda = c.T =2\pi c.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
Chọn B.

Trong mạch dao động thì i sớm pha hơn q là \(\frac{\pi}{2}.\)

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Đoạn mạch chỉ có cuộn cảm thuần thì i trễ pha \(\frac{\pi}{2}\)so với u.
\(I_0=\frac{U_0}{Z_L}=\frac{U_0}{\omega L}\)
Suy ra \(i=\frac{U_0}{\omega L}\cos\left(\omega t-\frac{\pi}{2}\right)\)

Câu 46: Tại lễ hội phim miễn phí ở Anh, có những rạp chiếu phim nhỏ mà điện năng sử dụng cho rạp hoàn toàn từ hệ thống xe đạp phát điện do chính khán giả vừa xem vừa đạp xe. Năng lượng từ các vòng quay của 12 chiếc xe đạp sẽ nạp điện cho những bộ ác quy 12V. Hệ thống này có thể sinh ra dòng điện đủ để chạy máy chiếu, đèn và dàn âm thanh. Nếu các khán giả đều đạp xe với tốc độ n vòng/phút thì công suất điện cung cấp chỉ đáp ứng 40% yêu cầu của rạp nếu các khán giả tăng tốc độ đạp xe thêm 5 vòng/phút thì công suất điện sinh ra đáp ứng được 60% yêu cầu của rạp. Để cung cấp đủ công suất điện cho rạp các khán giả cần tăng tốc độ đạp xe thêm ít nhất bao nhiêu vòng/ phút nữa?
A. 2,5 B. 8 C. 5 D. 10

\(Z_{L1}=\omega_1.L=30\) (1)
\(Z_{C1}=\dfrac{1}{\omega_1C}=40\) (2)
Lấy (1) chia (2) vế với vế ta được: \(\omega_1^2LC=\dfrac{3}{4}\) (3)
Khi tần số \(\omega_2\) thì hệ số công suất bằng 1
\(\Rightarrow Z_{L2}=Z_{C2}\Rightarrow \omega_2.L=\dfrac{1}{\omega_2C}\)
\(\Rightarrow \omega_{2}^2LC=1\) (4)
Lấy (4) chia (3) vế với vế \(\Rightarrow \dfrac{\omega_2}{\omega_1}=\dfrac{2}{\sqrt 3}\Rightarrow \omega_2=\dfrac{2}{\sqrt 3}\omega_1\)
Chọn B.
Chọn đáp án D
+ Nhiệt lượng tỏa ra: