Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

Chọn vật qui chiếu gắn với đoàn xe: vật (2). Trong chuyển động tương đối của người đi mô tô (vật(1)) đối với (2), người này đi được quãng đường l = l500m lượt đi cũng như lượt về.


Đáp án A
Chọn vật qui chiếu gắn với đoàn xe: vật (2). Trong chuyển động tương đối của người đi mô tô (vật(1)) đối với (2), người này đi được quãng đường l = l500m lượt đi cũng như lượt về.


Đổi: s=1500m=1,5km
t=5′24s=0,09h
Gọi vận tốc của chiếc mô tô là: x (km/h) (x>40)
Thì vận tốc của di chuyển của mô tô khi di chuyển ngược đến xe cuối cùng là: v1=x+v=x+40(km/h)
Nên thời gian để di chuyển ngược đến xe cuối cùng là:
t1=s/v1=1,5/x+40
Và vận tốc di chuyển của mô tô khi di chuyển trở về xe đầu tiên là:
v2=x−v=x−40(km/h) (vì mô tô di chuyển đuổi theo đoàn xe đang di chuyển cùng hướng nên vận tốc di chuyển so với đoàn xe sẽ bị giảm đi)
Nên thời gian di chuyển trở về xe đầu tiên là:
t2=s/v2=1,5/x−40(km/h)
Theo đề bài ta có cả thời gian đi và quay trở lại là 5'24s=0,09 h, hay:
\(t1+t2=t\Leftrightarrow\frac{1,5}{x+40}+\frac{1,5}{x-40}=0,09\)
\(\Leftrightarrow1,5\left(x-40\right)+1,5\left(x+40\right)=0,09\left(x+40\right)\left(x-40\right)\)
\(\Leftrightarrow1,5\left(x-40+x+40\right)=0,09\left(x^2-1600\right)\)
\(\Leftrightarrow3x=0,09x^2-144\)
\(\Leftrightarrow9x^2-300x-14400=0\)
\(\Leftrightarrow\left(x-60\right)\left(x+\frac{80}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-60=0\\x+\frac{80}{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=60\left(tm\right)\\x=\frac{-80}{3}\left(ktm\right)\end{matrix}\right.\)
Vậy vận tốc của chiếc mô tô là: 60km/h
Giải:
Đổi: s = 1500m =1,5km
t = 5′24s = 0,09h
Gọi vận tốc của chiếc mô tô là: x (km/h) (x>40)
Thì vận tốc của di chuyển của mô tô khi di chuyển ngược đến xe cuối cùng là: v\(_1\) = x + v= x + 40 (km/h)
Nên thời gian để di chuyển ngược đến xe cuối cùng là:
t\(_1\)= \(\frac{s}{v_1}\)= \(\frac{1,5}{x+40}\)
Và vận tốc di chuyển của mô tô khi di chuyển trở về xe đầu tiên là:
v\(_2\) = x − v = x − 40 (km/h)v (vì mô tô di chuyển đuổi theo đoàn xe đang di chuyển cùng hướng nên vận tốc di chuyển so với đoàn xe sẽ bị giảm đi)
Nên thời gian di chuyển trở về xe đầu tiên là:
t\(_2\)= \(\frac{s}{v_2}\) = \(\frac{1,5}{x-40}\) (km/h)
Theo đề bài ta có cả thời gian đi và quay trở lại là 5'24s=0,09 h, hay:
t\(_1\)+t\(_2\) = t ⇔ \(\frac{1,5}{x+40}\) + \(\frac{1,5}{x-40}\) = 0,09
⇔1,5 . ( x − 40 ) +1,5 . ( x + 40 ) = 0,09 . ( x + 40 ) . ( x − 40 ) ( quy đồng bỏ mẫu )
⇔1,5 . ( x − 40 + x + 40 ) = 0,09 (x\(^2\)− 1600 )
⇔3x = 0,09x\(^2\) − 144
⇔9x\(^2\) − 300x − 14400 = 0
⇔ ( x − 60 ) . ( x + \(\frac{80}{3}\))
⇔⎡ x − 60 = 0
⎣ x + \(\frac{80}{3}\)= 0
⇔⎡ x = 60 ( tm )
⎣ x = − \(\frac{80}{3}\) ( ktm )
Vậy vận tốc của chiếc mô tô là: 60km/h

Đổi : 1200m=1,2km
1min40'=1/36h
gọi:1 là chiến sĩ
2 là đoàn xe cơ giới
3 là đất
Chọn chiều dương là chiều chuyển động của đoàn,ta có
Khi chiến sĩ đi về cuối đoàn:v12=v13-v23=v13-18
=>t1=\(\frac{1,2}{v13-18}\)
Khi chiến sĩ đi về đầu đoàn:v12=v13+v23=v13+18
=>t2=\(\frac{1,2}{v13+18}\)
mà t1+t2=t
<=>\(\frac{1,2}{v13-18}+\frac{1,2}{v13+18}\)=\(\frac{1}{36}\)
giải phương trình trên ta dược v13=90km/h
Vậy vận tốc của chiến sĩ đi mô tô là 90km/h
*không biết có đúng hay ko nữa
Gọi vận tốc của người đó so vs đoàn người là v12
=> vận tốc ng đó so vs mặt đất: v13
Vận tốc của người đó khi đi ngược chiều so vs đoàn người\(\overrightarrow{v_{23}}=\overrightarrow{v_{21}}+\overrightarrow{v_{13}}=\overrightarrow{v_{13}}-\overrightarrow{v_{12}}\)
\(\Rightarrow v_{12}=\sqrt{v_{13}^2+v_{23}^2+2.v_{13}.v_{23}.\cos180^0}=\left|v_{13}-v_{23}\right|\)
Vận tốc của người đó khi đi cùng chiều:
\(v_{12}=\sqrt{v_{13}^2+v_{23}^2+2.v_{13}.v_{23}.\cos0^0}=v_{13}+v_{23}\)
Thời gian đi từ đầu hàng đến cuối hàng:
\(t_1=\frac{L}{v_{12}}=\frac{1200}{v_{13}-5}\)
Thời gian ng đó đi từ cuối hàng lên đầu hàng:
\(t_2=\frac{L}{v_{12}'}=\frac{1200}{v_{13}+v_{23}}=\frac{1200}{v_{13}+5}\)
Có t1+t2= 100(s)
\(\Rightarrow\frac{1200}{v_{13}-5}+\frac{1200}{v_{13}+5}=100\)
tự giải nốt =.=

1/ gọi t1 là thời gian ô tô chạy 1/3 quãng đường đầu
=> t1 = s / ( 3 * v1 ) = s / 120
gọi t2 là thời gian ô tô chạy 1/3 quãng đường tiếp theo
=> t2 = s / ( 3 * v2 ) = s / 150
gọi t3 là thời gian ô tô chạy 1/3 quãng đường cuối cùng
=> t3 = s / ( 3 * v3 )
ta có v tb = s / t = s / ( s / 120 + s / 150 + s / ( 3 *v3) )
=> 45 = s / [s ( 1/ 120 + 1/ 150 + 1/ ( 3 *v3 ) ) ]
=> 45 = 1 / ( 3 / 200 + 1 / ( 3 * v3 )
=> 1 / 45 = 3 / 200 + 1/ ( 3 * v3 )
=> 1 / ( 3 *v3 ) = 1 / 45 - 3 / 200
=> 1 / ( 3 *v3 ) = 13 / 1800
=> 3 * v3 = 1800 / 13
=> v3 = 1800 / 39 = khoảng 46,15 km / h
2/Tính vận tốc trung bình của xe đi từ A đến B
vtb = s/t
theo bài ra ta có : s/2 = 20*t1 và s/2 = 60*t2
=> vtb = s/( t1 + t2) = s/ ( s/40 + s/ 120 ) = 30 (km/h)
Tính vận tốc trung bình của xe đi từ B đến A
theo bài ra ta cũng có
t/2 = s1/20 và t/2 = s2/60
=> vtb" = (s1 + s2 )/t = ( 10t + 30t )/t = 40 ( km/h)
Mà nếu xe từ B xuất phát muộn hơn so với xe xuất phát từ A 30phút = 1/2 h thì 2 xe đến địa điểm cùng 1 lúc
=> sA-B = 30*t
sB-A = 40 * ( t - 1/2)
Mà sA-B = sB-A => 30*t = 40 * ( t - 1/2) => t= 2 (h)
Vậy s = 60 ( km)

bài 1: Chọn chiều dương là chiều chuyển động, góc thời gian lúc xe 1 bắt đầu cđ.
pt cđ của xe 1: x1= v01.t + a1.t2/2 = 0,25.t2
pt cđ của xe 2: x1= v02.t = 10t
Khi xe 1 đuổi kịp xe 2: x1=x2 <=> 0,25.t2=10t <=> t = 40s
=> S1 = 0,25.402=400m ; v1 = 0,5.40 = 20 m/s
bài 2: Chọn chiều dương là chiều cđ, góc thời gian lúc xe ô tô khởi hành từ A.
ptvt xe 1: v1 = 0,5.t ; ptvt xe 2: v2 = 5 + 0,3t
ptcđ xe 1: x1 =-0,25.t2 ; ptcđ xe 2: x2 = -125 + 5t + 0,15.t2
a. gặp nhau <=> x1 = x2 <=>-0,25.t2 = -125 + 5t + 0,15.t2 <=> t = 18,3s
vị trí gặp nhau: |-0,25*t2| = 84m -> cách A 84m
v1 = ... ; v2 = ....
b. xe từ A -> B:-125 = -0,25.t2 <=> t = 10\(\sqrt{5}\)s => xe A đi được 125m
=>qđ xe từ B đi được: x2 = 61,8m
Chọn A
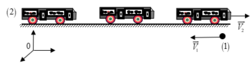
+ Chọn hệ quy chiếu gắn với đoàn xe: vật (2).
+ Trong chuyển động tương đối của người đi mô tô (vật (1) đối với (2), người này đi được quãng đường l = 1500 m lượt đi cũng như lượt về.
+ Ta có:
+ Chọn chiều dương là chiều chuyển động của (1) ta có tốc độ tương đối:
+ Theo đề bài suy ra:
+ Vận tốc v 1 là nghiệm dương của phương trình bậc hai: