Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Cảm kháng của cuộn dây Z L = L ω = 200 Ω
Thay đổi C đến giá trị C 1 thì điện áp u vuông pha với điện áp u R L → U C m a x khi đó
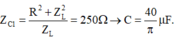

Đáp án D
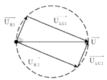
+ Biểu diễn vecto các điện áp.
→ Với trường hợp ![]() ta dễ dàng tìm được:
ta dễ dàng tìm được:
![]()

Đáp án A
Phương pháp: Ta có: Khi L = L1 thì UAM1 = UR1 = U Khi L = L2 thì
![]()
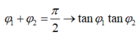
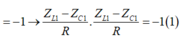
Mặt khác: ta có:
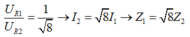
![]()
![]()
Chia cả hai vế của (2) cho (ZL2 - ZC) kết hợp với (1), Ta được:
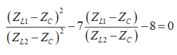
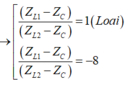
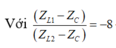
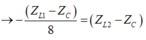
Thay vào (1)
![]()
Hệ số công suất của mạch khi L=L:
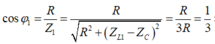
=>Chọn A

\(Z_L=\omega L=100\Omega\)
Ta áp dụng một tính chất của mạch RLC khi C thay đổi để Uc max là lúc đó u mạch vuông pha với uRL.
Như vậy, bài này theo giả thiết uAB lệch pha pi/2 so với uAM là thỏa mãn điều kiện trên.
=> \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{50^2+100^2}{100}=125\Omega\)
=> C

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Chọn B
Độ lệch pha giữa hai đầu đoạn mạch AM và i là:
tan φ A M = Z L R
Độ lệch pha giữa hai đầu đoạn mạch AB và i là:
tan
φ
A
B
=
Z
L
-
Z
C
R
Để AM và AB lệch pha nhau góc
π
2
tan φ A M . tan φ A B = - 1 ⇒ C = 8 . 10 - 5 π F


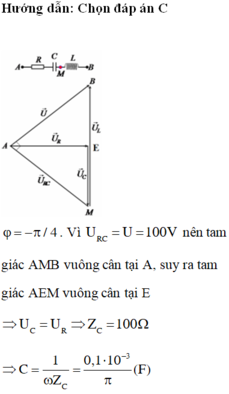
Chọn D
tanφAB. tanφAM = -1 ⇔ Z L - Z C R . Z L R = -1
⇔ R2=ZL(ZC – ZL) = ωL( 1 ω C - ω L )
⇔ R2= L C - ω 2 L 2 ⇔ ω = L - R 2 C L 2 C