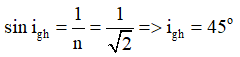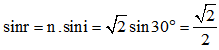Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta áp dụng vào công thức: F=\(BIl\)sinα, F cực tiểu khi sinα=0 hay α=00
vậy đáp án là A

Mặt phẳng khung dây hợp với đường cảm ứng từ một góc 300 => α= 600
\(\left|\phi\right|=\left|NBScos\alpha\right|=\left|1.5.10^{-2}.12.10^{-4}.cos60^0\right|=3.10^{-5}\)Wb

Vì tia sáng tới có đường kéo dài qua O nên tia tới SI vuông góc mặt phẳng trụ ⇒ góc i = 0 ⇒ tia sáng sẽ truyền thẳng vào khối trong suốt tới O.
Tại O: tia sáng SO tạo với pháp tuyến ON của mặt phân cách phẳng một góc tới i.
Ta có: i = 90o - α
Mặt khác, góc giới hạn khi ánh sáng truyền từ khối bán trụ ra không khí được tính bởi công thức:
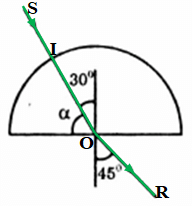
a) α = 60o
→ i = 90o – α = 30o → i < igh
Áp dụng định luật khúc xạ:
→ r = 45o. Vậy tia khúc xạ hợp với pháp tuyến của mặt phẳng phân cách của khối bán trụ góc khúc xạ 45o như hình vẽ.
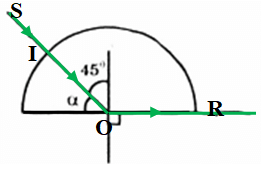
b) α = 45o
→ i = 90o – α = 45o → i = igh
→ r = 90o → Tia khúc xạ đi sát mặt phân cách của khối tròn như hình vẽ:
c) α = 30o
→ i = 90o – α = 60o → i > igh
→ Xảy ra phản xạ toàn phần, không có tia khúc xạ ra ngoài không khí. Đường đi của tia sáng được vẽ trên hình:

a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(