Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
\(f=2f_0=100\left(Hz\right)\)
\(l=\frac{k\lambda}{2}=\frac{kv}{2f}\Rightarrow v=\frac{2lf}{k}\) ( vì vật được kích thích bằng nam châm)
\(=\frac{2.0,9.100}{6}=30\left(m/s\right)\)
Ta có:
Trong 1 (s) ứng với 50 chu kì mà mỗi chu kì có độ lớn 1 (A) 4 lần
⇒ 50 chu lì có 50.4 = 200 (lần)
T=1f=0,02T=1f=0,02
t =1s = 50T
trị tuyệt đối = 1 -- I = 1 và I = -1
--> có 200 lần
Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.
\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)
\(E=\frac{1}{2}\omega^2A^2\) nên vận tốc truyền sóng không ảnh hưởng.
chọn D
\(u=2\cos\left(20\pi\left(t-\frac{x}{25}\right)\right)=2\cos\left(20\pi t-\frac{4\pi x}{5}\right)\)
\(\Rightarrow\lambda=\frac{5}{2}\left(m\right)=250\left(cm\right)\)
\(f=\frac{\omega}{2\pi}=\frac{20\pi}{2\pi}=10\left(Hz\right)\)
\(\Rightarrow v=f.\lambda=10.250=2500\left(cm/s\right)=25\left(m/s\right)\)
Đáp án C
Ta có:
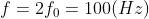
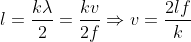( vì vật được kích thích bằng nam châm)
