Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Dây thứ nhất có: l 1 = 100m, S 1 = 1 m m 2 , R 1 = 1,7Ω
Dây thứ hai có: l 2 = 200m, S 2 = ?, R 2 = 17Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 2 =200m nhưng lại có tiết diện S 3 = S 1 = 1 m m 2 .
Như vậy dây 1 và dây 3 có cùng vật liệu và tiết diện nhưng khác chiều dài.
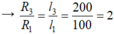
→ R 3 = 2 . R 1 = 3,4Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng chiều dài, khác tiết diện.
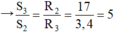
→ S 2 = S 3 / 5 = 1/5 = 0,2 m m 2

chọn dây đồng thứ 3 có S3=S1, có l3=l2
xét dây thứ nhất: \(=>\dfrac{R1}{R3}=\dfrac{l1}{l3}=>\dfrac{160}{R3}=\dfrac{100}{300}=>R3=480\Omega\)
xét dây thứ 2: \(=>\dfrac{R2}{R3}=\dfrac{S3}{S2}=>\dfrac{40}{480}=\dfrac{0,2}{S2}=>S2=2,4mm^2\)

Tóm tắt
\(l_1=100m\\ S_1=1mm^2\\ R_1=1,7\Omega\\ l_2=200m\\ R_2=17\Omega\)
__________
\(S_2=?mm^2\)
Giải
Vì R tỉ lệ thuận với l và tỉ lệ nghịch với S
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}\cdot\dfrac{S_2}{S_1}\\ \Leftrightarrow\dfrac{1,7}{17}=\dfrac{100}{200}\cdot\dfrac{S_2}{1}\\ \Leftrightarrow S_2=0,2mm^2\)

\(R_2=\rho\dfrac{l_2}{S_2}\Rightarrow\rho=\dfrac{R_2.S_2}{l_2}=\dfrac{8.0,1.10^{-6}}{10}=8.10^{-8}\left(\Omega.m\right)\)
\(R_1=\rho\dfrac{l_1}{S_1}=8.10^{-8}.\dfrac{20}{0,4.10^{-6}}=4\left(\Omega\right)\)

Dây thứ nhất có: l1 = 200m, S1 = 0,2mm2, R1 = 120Ω
Dây thứ hai có: l2 = 50m, S2 = ? mm2, R2 = 45Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l3 = l2 =50m nhưng lại có tiết diện S3 = S1 = 0,2 mm2.
Như vậy dây 1 và dây 3 có cùng vật liệu và tiết diện, khác chiều dài
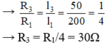
→ R3 = R1/4 = 30Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng chiều dài, khác tiết diện →
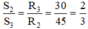
→ S2 = 2S3/3 = 2.0,2/3 = 2/15mm2 = 0,133mm2.
Lưu ý: Qua hai bài trên ta nhận thấy, với hai dây dẫn cùng vật liệu nhưng có chiều dài và tiết diện khác nhau thì ta có thể dùng hệ thức liên hệ sau để làm nhanh hơn.
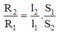

Dây thứ nhất có: l1 = 100m, S1 = 0,1 mm2, R1 = 500Ω
Dây thứ hai có: l2 = 50m, S2 = 0,5 mm2, R2 = ? Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l3 = l1 =100m nhưng lại có tiết diện S3 = S2 = 0,5 mm2.
Như vậy dây 1 và dây 3 có cùng vật liệu và chiều dài, khác tiết diện →
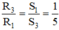
→ R3 = R1/5 = 100Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng tiết diện, khác chiều dài →
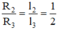
→ R2 = R3/2 = 100/2 = 50Ω

\(R_1=\rho\dfrac{l_1}{S_1}\Rightarrow\rho=\dfrac{R_1.S_1}{l_1}=\dfrac{160.0,2.10^{-6}}{100}=3,2.10^{-7}\left(\Omega.m\right)\)
\(R_2=\rho\dfrac{l_2}{S_2}\Rightarrow S_2=\dfrac{\rho.l_2}{R_2}=\dfrac{3,2.10^{-7}.300}{40}=2,4.10^{-6}\left(m^2\right)\)

a. \(\left[{}\begin{matrix}R1=p1\dfrac{l1}{S1}=0,4.10^{-6}\dfrac{100}{0,5.10^{-6}}=80\left(\Omega\right)\\R2=p2\dfrac{l2}{S2}=0,4.10^{-6}\dfrac{100}{0,5S1}=0,4.10^{-6}\dfrac{100}{0,5.0,5.10^{-6}}=160\left(\Omega\right)\end{matrix}\right.\)
b. \(I=I1=I2=\dfrac{U}{R}=\dfrac{40}{80+160}=\dfrac{1}{6}\left(A\right)\left(R1ntR2\right)\)
\(\Rightarrow\left[{}\begin{matrix}U1=I1.R1=\dfrac{1}{6}.80=\dfrac{40}{3}\left(V\right)\\U2=I2.R2=\dfrac{1}{6}.160=\dfrac{80}{3}\left(V\right)\end{matrix}\right.\)

\(R2=p2\dfrac{l2}{S2}\Rightarrow l2=\dfrac{R2.S2}{p2}=\dfrac{100.0,2.10^{-6}}{1,7.10^{-8}}\simeq1176,5\left(m\right)\)