Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(R=\rho\cdot\dfrac{l}{S}\)
Mà \(R'=\rho\cdot\dfrac{l'}{S}=\rho\cdot\dfrac{\dfrac{l}{2}}{S}=\dfrac{1}{2}R\)
\(\Rightarrow R'=\dfrac{1}{2}\cdot12=6\Omega\)

Chọn D
Khi gập đôi sợi dây thì dây mới có chiều dài giảm đi 2 lần và tiết diện tăng gấp 2 lần. Chiều dài giảm 2 lần nên điện trở giảm hai lần, tiết diện tăng 2 lần nên điện trở giảm thêm 2 lần nữa kết quả là giảm 4 lần. Vì vậy điện trở dây dẫn mới là 8:4 = 2Ω.

Do dây dẫn được gập đôi lại nên chiều dài giảm đi 2 lần và tiết diện tăng 2 lần.
Chiều dài giảm 2 lần nên điện trở giảm 2 lần, tiết diện tăng 2 lần nên điện trở giảm 2 lần. Kết quả là giảm 4 lần.
Vì vậy điện trở dây dẫn mới là: 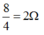
→ Đáp án D

Theo đề bài, ta có: \(\left\{{}\begin{matrix}\rho=\rho'\\l=l'\\S'=2S\\R=?\end{matrix}\right.\)
Từ công thức \(R=\rho.\dfrac{l}{S}\rightarrow\rho=\dfrac{R.S}{l}\)
\(\rho=\rho'\\ \rightarrow\dfrac{R.S}{l}=\dfrac{R'.S'}{l}\\ \rightarrow R.S=R'.S'\\ \rightarrow R.S=R'.2S'\\ \rightarrow R=2.R'\\ \rightarrow R'=\dfrac{R}{2}\)
Vậy điện trở giảm 1 nửa
\(\rightarrow D\) Giảm đi 2 lần
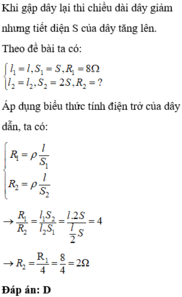

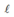
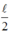
giảm 4 lần
C