Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Trước hết ta có kết quả: Khối tứ diện ABCD có thể tích được tính theo công thức
![]()
Áp dụng kết quả này, ta có
![]()
= 6h
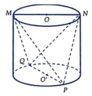
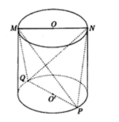
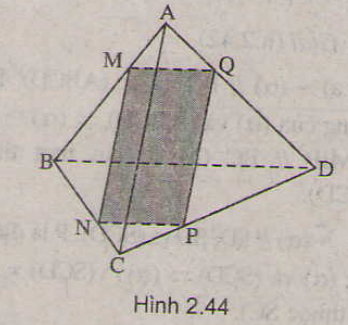
trong đó MN = PQ = 6 dm và h = d(MN;PQ) là chiều cao của hình trụ.
Từ giả thiết ta có h = 5 dm
Suy ra thể tích khối trụ là ![]() , với r = 3 dm
, với r = 3 dm
Do đó thể tích của lượng đá bị cắt bỏ là
![]()
Vậy phương án đúng là B.
Phân tích phương án nhiễu.
Phương án A và C: Sai do HS giải đúng nhưng làm tròn số bị sai hoặc lấy
Phương án D: Sai do HS chọn π = 3,141

Đáp án C
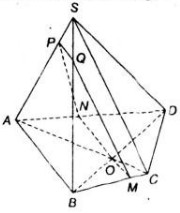
Tứ diện ABCD có chiểu cao không đổi do đó thể tích nhỏ nhất khi diện tích tam giác ABC nhỏ nhất. Vì AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện nên tâm I của mặt cầu nằm trong tam giác ABC
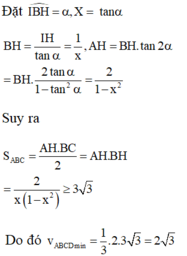
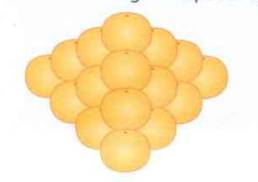








Ta sử dụng phương pháp thử và sai, bắt đầu với n = 1 và tăng giá trị của n cho đến khi 1/6n(n+1)(n+2) vượt quá 100. Khi đó, n - 1 sẽ là số lớp tối đa của khối tứ diện.
Thử nghiệm:
- Với n = 1: 1/6 x 1 x 2 x 3 = 1, không vượt quá 100.
- Với n = 2: 1/6 x 2 x 3 x 4 = 4, không vượt quá 100.
- Với n = 3: 1/6 x 3 x 4 x 5 = 10, không vượt quá 100.
- Với n = 4: 1/6 x 4 x 5 x 6 = 20/3, vượt quá 100.
Vậy, số lớp tối đa của khối tứ diện được xếp từ 100 quả cam là n - 1 = 3.
Dùng AI hay sao 20/3 > 100 hay thế bạn =))