Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác vuông \(PQR\) có:
\(\widehat P + \widehat Q + \widehat R = 180^\circ \Leftrightarrow \widehat P + 90^\circ + 42^\circ = 180^\circ \Rightarrow \widehat P = 180^\circ - 90^\circ - 42^\circ = 48^\circ \)
Xét tam giác vuông \(UVT\) có:
\(U{V^2} = U{T^2} + V{T^2} \Leftrightarrow {6^2} = U{T^2} + {4^2} \Rightarrow U{T^2} = {6^2} - {4^2} = 20 \Rightarrow UT = 2\sqrt 5 \)
Xét tam giác vuông \(DEF\) có:
\(E{F^2} = D{E^2} + D{F^2} \Leftrightarrow E{F^2} = {9^2} + {12^2} \Rightarrow E{F^2} = 225 \Rightarrow EF = 15\)
Xét tam giác vuông \(MNK\) có:
\(K{N^2} = K{M^2} + M{N^2} \Leftrightarrow {9^2} = K{M^2} + {6^2} \Rightarrow K{M^2} = {9^2} - {6^2} = 45 \Rightarrow KM = 3\sqrt 5 \)
Xét tam giác vuông \(IGH\) có:
\(I{H^2} = H{G^2} + I{G^2} \Leftrightarrow I{H^2} = 7,{5^2} + {10^2} \Rightarrow I{H^2} = 156,25 \Rightarrow IH = 12,5\)
- Xét \(\Delta ABC\) và \(\Delta QPR\) có:
\(\widehat B = \widehat P = 48^\circ \) (chứng minh trên)
\(\widehat A = \widehat Q = 90^\circ \)
Do đó, \(\Delta ABC\backsim\Delta QPR\) (g.g)
- Xét \(\Delta UTV\) và \(\Delta KMN\) có:
\(\widehat T = \widehat M = 90^\circ \)
\(\frac{{UT}}{{KM}} = \frac{{2\sqrt 5 }}{{3\sqrt 5 }} = \frac{2}{3};\frac{{VT}}{{MN}} = \frac{4}{6} = \frac{2}{3}\)
Do đó, \(\Delta UTV\backsim\Delta KMN\) (c.g.c)
- Xét \(\Delta DEF\) và \(\Delta GHI\) có:
\(\widehat D = \widehat G = 90^\circ \)
\(\frac{{HG}}{{DE}} = \frac{{7,5}}{9} = \frac{5}{6};\frac{{IG}}{{DF}} = \frac{{10}}{{12}} = \frac{5}{6}\)
Do đó, \(\Delta DEF\backsim\Delta GHI\) (c.g.c).

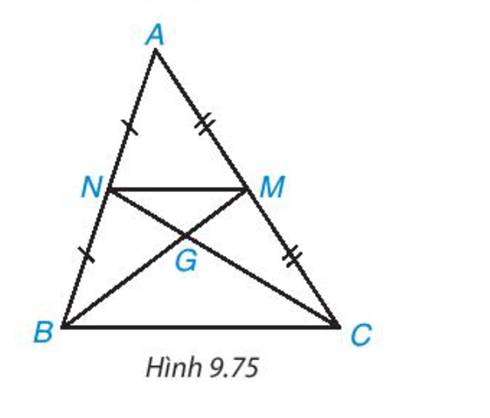
- Xét tam giác ABC có, NA=NB, MA=MC
=> NM là đường trung bình của tam giác ABC
=> NM // BC, \(NM = \frac{1}{2}AB\)
- Xét tam giác GMN và tam giác GBC có NM // BC => ΔGMN ∽ ΔGBC

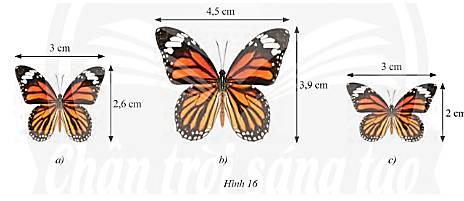
- Xét hình 16a và hình 16b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16a và hình 16b lần lượt là:
\(\frac{3}{{4,5}} = \frac{2}{3};\frac{{2,6}}{{3,9}} = \frac{2}{3}\). Do đó, tồn tại hình động dạng phối cảnh của hình 16a bằng hình 16b. Do đó, hình 16a và hình 16b đồng dạng với nhau.
- Xét hình 16b và hình 16c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16b và hình 16c lần lượt là:
\(\frac{{4,5}}{3} = 1,5;\frac{{3,9}}{2} = 1,95\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 16b để bằng hình 16c. Do đó, hình 16b và hình 16c không đồng dạng với nhau.
- Xét hình 16c và hình 16c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16a và hình 16c lần lượt là:
\(\frac{3}{3} = 1;\frac{{2,6}}{2} = 1,3\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 16a để bằng hình 16c. Do đó, hình 16a và hình 16c không đồng dạng với nhau.

Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.

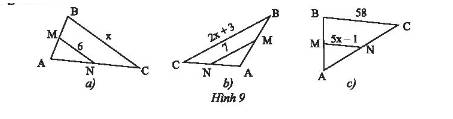
- Hình a:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)
- Hình b:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)
\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).
- Hình c
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]
\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].
a: MN là đường trung bình
=>MN=BC/2
=>x=6*2=12
b: MN là đường trung bình
=>2x+3=2*7=14
=>2x=11
=>x=11/2
c: MN là đường trung bình
=>5x-1=58/2=29
=>5x=30
=>x=6

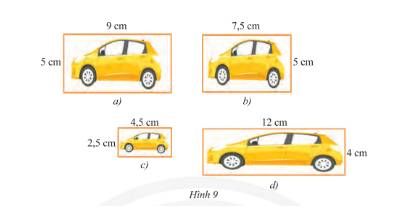
- Xét hình 9a và hình 9b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9b lần lượt là:
\(\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 9b. Do đó, hình 9a và hình 9b không đồng dạng với nhau.
- Xét hình 9a và hình 9c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9c lần lượt là:
\(\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2\). Do đó, tồn tại hình động dạng phối cảnh của hình 9a bằng hình 9c (hình 9a thu nhỏ với tỉ số 2). Do đó, hình 9a và hình 9c đồng dạng với nhau.
- Xét hình 9a và hình 9d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9d lần lượt là:
\(\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 9b. Do đó, hình 9a và hình 9b không đồng dạng với nhau.

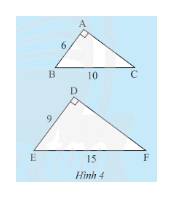
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)



Quan sát hình vẽ ta thấy, cạnh ngắn nhất của tam giác \(ABC\) là cạnh \(AC\);cạnh ngắn nhất của tam giác \(DEF\) là cạnh \(DF\).
Do đó, ta có: \(\frac{{AC}}{{DF}} = \frac{{600}}{{300}} = 2\).
Do đó, tỉ số chu vi của tam giác \(ABC\) và tam giác \(DEF\) là 2.
Chu vi tam giác \(DEF\) là: \(300 + 350 + 550 = 1200m\)
Chu vi tam giác \(ABC\) là: \(1200.2 = 2400m\).
Quãng đường bạn Nam đã chạy là: \(1200.4 = 4800m\)
Quãng đường bạn Hùng đã chạy là: \(2400.2 = 4800m\).
Do đó, hai bạn Nam và Hùng đã chạy hai quãng đường bằng nhau.