Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ
vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
Đáp án B
Phân tích:
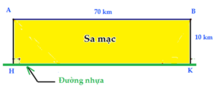
● Ta có thể mô tả bài toán trên bằng hình vẽ sau:
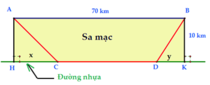
● Như đã phân tích ở trên, nếu đi trực tiếp từ A đến B trên sa mạc với vận tốc và khoảng cách hiện có thì nhà địa chất học không thể đến đúng thời gian quy định
● Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn:
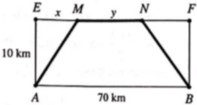
Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)
Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)
Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).
Goi H, K, C, D là các điểm như hình vẽ.
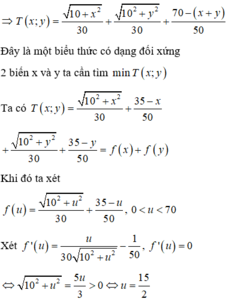
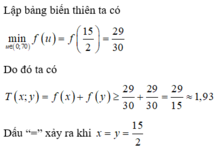
Giải:
Nếu di chuyển dấu phẩy của số thập phân a sang phải 2 đơn vị tứa là nhân số thập phân a với 100.
Gọi số a (cũ) là 1 phần thì số a (mới) là 100 phần.
Vậy tổng số phần bằng nhau tương ứng với 17043, 952 là 1 + 100 = 101 (phần)
Và số a ban đầu cần tìm là :
17043, 952 : 101 = 168, 752
Vậy số thập phân ban đầu là 168, 752.
ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a
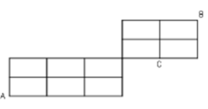
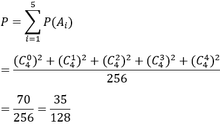
Đáp án A
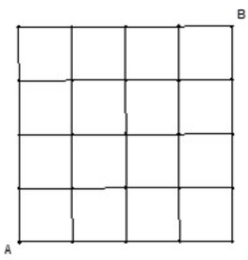
Phương pháp: Chia đường đi của thỏ thành 2 giai đoạn, tính số phần tử của không gian mẫu và số phần tử của biến cố A « thỏ đến được vị trí B » .
Cách giải :
Từ A đến B nhất định phải đi qua D,
ta chia làm 2 giai đoạn A → D