Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Dao động cơ là sự chuyển động có giới hạn trong không gian của một vật quanh một vị trí xác định. Dao động được mô tả theo định luật hình sin (cos) theo thời gian
Dao động đó có thể được mô tả bằng lời hoặc thông qua các phương trình toán học dựa vào các thông tin như biên độ, li độ, tần số, chu kì.

a)
Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,02}=50Hz\)
b)
\(N=\dfrac{t}{T}=\dfrac{10}{0,02}=500\) (dao động)
a) Để tính tần số của dao động, ta dùng công thức:
Tần số (f) = 1 / Chu kì (T)
Trong trường hợp này, chu kì (T) là 0.02s.
Vậy, tần số của dao động là:
f = 1 / 0.02 = 50 Hz
b) Để tính số dao động thực hiện trong 10s, ta dùng công thức:
Số dao động = Thời gian (t) / Chu kì (T)
Trong trường hợp này, thời gian (t) là 10s và chu kì (T) là 0.02s.
Vậy, số dao động thực hiện trong 10s là:
Số dao động = 10 / 0.02 = 500 lần.

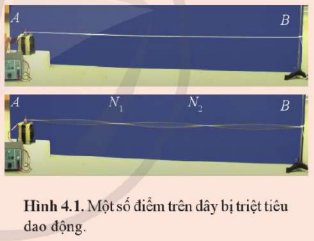
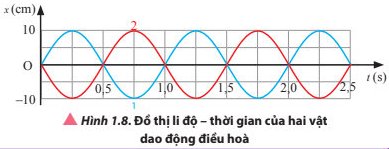
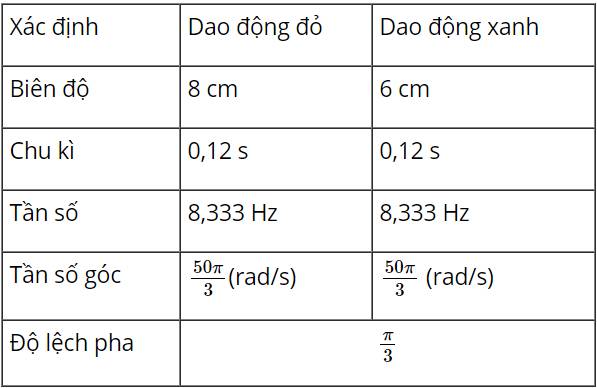
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.

Để xác định biên độ, tần số góc, chu kì và pha ban đầu của động, ta cần phân tích công thức của dao động và so sánh với công thức tổng quát.Công thức tổng quát của một dao động harmonic là:x = A * cos(ωt + φ)Trong đó:- x là vị trí của đối tượng tại thời điểm t.- A là biên độ của dao động.- ω là tần số góc của dao động.- t là thời gian.- φ là pha ban đầu của dao động.Trong công thức đã cho:x = -5cos(10πt + π/2)cmSo sánh với công thức tổng quát, ta có:A = -5 cm (biên độ)ω = 10π rad/s (tần số góc)φ = π/2 rad (pha ban đầu)Như vậy, biên độ của dao động là -5 cm, tần số góc là 10π rad/s, chu kì của dao động là T = 2π

Biên độ: A=8
Pha ban đầu: pi
Chu kì: \(T=\dfrac{2pi}{4pi}=\dfrac{1}{2}\)
Tần số góc là 4pi

a) Biên độ dao động A=0,2 cm
Chu kì T=0,4 s
Tần số \(f = \frac{1}{T} = \frac{1}{{0,4}} = 2,5Hz\)
Tần số góc của dao động \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi rad/s\)
b) Li độ của vật dao động tại các thời điểm t1, t2, t3 ứng với các điểm A, B, C trên đường đồ thị li độ – thời gian lần lượt là x1=-0,1 cm, x2= -0,2 cm, x3= 0 cm.
c) Vì gốc thời gian trùng với vị trí cân bằng nên li độ cũng chính là độ dịch chuyển từ vị trí cân bằng đến vị trí của vật tại các điểm A, B, C.





Cánh ong mật này thực hiện 300 dao động trong 1s
Chu kì dao động của cánh ong là: \(T=\dfrac{1}{f}=\dfrac{1}{300}=0,003s\)