Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Thế năng đàn hồi : Thế năng đàn hồi :
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: ![]()
Biên độ dao động của con lắc: A = 7,5 - Δl0 = 7,5 - 2,5 = 5cm
Ta có: Δl0< A
Chọn chiều dương hướng xuống
=> Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo hông giãn cũng hông nén: Δl = 0
Thế năng đàn hồi tại vị trí đó: 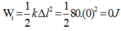


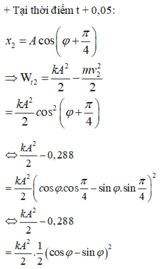


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

+ Phương trình dao động của hai con lắc lò xo
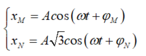
Khoảng cách giữa hai vật nặng của hai con lắc lò xo tại thời điểm t là:
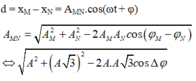
Trong quá trình dao động, độ chênh lệch độ cao lớn nhất của hai vật là A
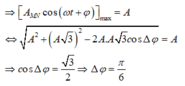
Động năng của con lắc M cực đại W đ m = k A 2 2 = 0 , 12 J khi vật M ở VTCB. Khi đó ta biểu diễn được vị trí của vật N được biểu diễn trên đường tròn lượng giác (M và N lệch pha nhau góc π/6).
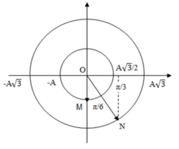
+ Từ đường tròn lượng giác xác định được

Đáp án D

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
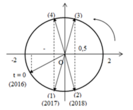
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
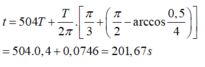
Đáp án C

Lò xo giãn: \(A->N;P->A\)
Lò xo nén: \(N->P\)
Lực đàn hồi cùng chiều với lực kéo về: \(A->M;N->P;Q->A\)
Lực đàn hồi ngược chiều với lực kéo về: \(M-N;P->Q\)
Tỉ số thời gian giãn cho thời gian nén là \(\frac{^{T_D}}{^{T_N}}=2.\left(1\right)\)
Nhìn trên hình vẽ ta có thấy:
Thời gian ngược chiều ( \(M->N;P->Q\) ) + Thời gian nén ( N -> P ) = \(\frac{T}{2}\) (chính là thời gian đi nửa cung hình tròn)
còn lại bạn tham khảo ở : Câu hỏi của Phạm Hoàng Phương - Học và thi online với HOC24

Chọn đáp án D
@ Lời giải:
+ Thế năng của vật dao động điều hòa biến thiên tuần hoàn với tần số góc:
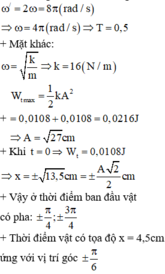
+ Vậy thời điểm vật qua vị trí x = 4,5cm lần đầu tiên là: T 24 = 1 48 s

Chọn đáp án A
@ Lời giải:
+ Tần số ngoại lực cưỡng bức bằng tần số hệ dao động cưỡng bức.
+ Tốc độ cực đại vmax= ꞷA = 10π.5 = 50π cm/s
ü Chọn đáp án A

Ta có:\(\Delta\)l=4cm;A=8cm;T=2\(\pi\)\(\sqrt{\frac{\Delta l}{g}}\)=0,4(s)
2\(\alpha\)=\(\omega\)\(\Delta\)t nén
\(\Rightarrow\)\(\Delta\)t nén =\(\frac{2\alpha}{\omega}\)=\(\frac{2arccos\frac{\Delta l}{A}}{\frac{2\pi}{T}}\)=\(\frac{2.\frac{\pi}{3}}{2\pi}\).o,4=\(\frac{2}{15}\)(s)
Có j sai sót mong mn giúp đỡ![]()
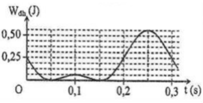

Giải thích: Đáp án D
Phương pháp: Sử dung̣ lý thuyết về thế năng đàn hồi của con lắc lò xo kết hợp kĩ năng đọc đồ thi ̣
Cách giải:
+ Bài này đã chọn mốc thế năng tại vị trí lò xo không biến dạng.
+ Từ đồ thị => Wtdh có độ chia nhỏ nhất: 0,25/4 = 0,0625 J.
+ Tại vị trí cao nhất thế năng đàn hồi:
+ Tại vị trí thấp nhất thế năng đàn hồi cực đại:
+ Lấy (2) chia (1):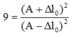
+ Từ đồ thị Chu kì dao động của con lắc: T = 0,3 s.
+ Ta có: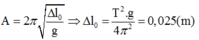
+ Tại VTCB: