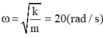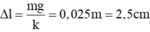Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,25}}=20\) (rad/s)
Độ dãn tại VTCB:
\(\Delta l=\dfrac{mg}{k}=\dfrac{0,25\cdot10}{100}=0,025m=2,5cm\)
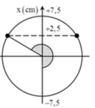
Lò xo kéo xuống dưới giãn 7,5cm.
\(\Rightarrow\)Biên độ: \(A=7,5-2,5=5cm=0,05m\)
Tại thời điểm ban đầu \(t=0\): \(x=-A\)\(\Rightarrow\varphi=\pi\)
Vậy pt là \(x=5cos\left(20t+\pi\right)cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,25}}=20\) (rad/s)
\(F_k=P\Rightarrow\Delta l.k=mg\Rightarrow\Delta l=\dfrac{mg}{k}=\dfrac{0,25.10}{100}=0,025\left(m\right)\)
Ta có : \(A+\Delta l=7,5\left(cm\right)\) \(\Rightarrow A=7,5-2,5=5\left(cm\right)\)
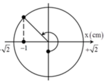
Trục Ox thẳng đứng ; chiều (+) hướng lên ; gốc tọa độ ở VTCB t0 = 0 lúc thả vật \(\Rightarrow\varphi=-\pi\)
Phương trình dao động là : \(x=5.cos\left(20t-\pi\right)\)

+ Độ biến dạng của lò xo tại vị trí cân bằng
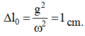
Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều dương. Thời điểm lò xo không biến dạng lần đầu tiên ứng với li độ x = - ∆ l = - 1 cm
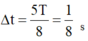
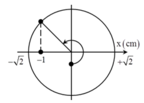
Đáp án D

Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hòa
Cách giải :
Vị trí cân bằng lò xo dãn một đoạn ∆ ε , ta có:
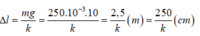
Vật được thả nhẹ từ vị trí lò xo dãn 6,5cm => biên độ dao động: A = 6,5 - 250 k
Vì A < 6,5cm nên dựa vào đáp án ta chọn A = 4cm
![]()
=> Phương trình dao động của vật: x = 4cos(20t) (cm)