Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án D
Phương pháp: Con lắc đơn và con lắc lò xo chịu thêm tác dụng của lực quán tính
Cách giải:
Vì thang máy chuyển động nhanh dần đều xuống phía dưới nên hai con lắc cùng chịu tác dụng của lực quán tính hướng lên phía trên.
* Xét với con lắc đơn:
+ Lúc này gia tốc trọng trường hiệu dụng tác dụng lên con lắc đơn là: g1 = g – a = 10 – 2,5 = 7,5 (m/s2)
+ Lúc qua VTCB, con lắc đơn có tốc độ và gia tốc trọng trường hiệu dụng g nên sau đó sẽ dao động với biên độ là: 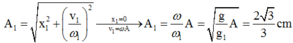
* Xét với con lắc lò xo:
+ Con lắc lò xo chịu tác dụng của lực quán tính hướng lên nên VTCB dịch chuyển lên phía trên so với VTCB ban đầu một đoạn: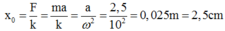
Do đó thời điểm tác dụng lực, con lắc lò xo có li độ x2=x0=2,5cm và tốc độ v2=ωA nên sau đó sẽ dao động với biên độ là: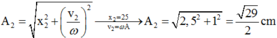
+ Tỉ số giữa biên độ dài của con lắc đơn và con lắc lò xo khi đó là: 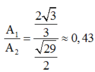

Độ biến dạng của lò xo tại vị trí cân bằng: $x=\Delta l=\dfrac{mg}{k}=\dfrac{T^2 g}{4\pi ^2} = 4cm.$
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí $x=\Delta l.$
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng: $y=\Delta l=\dfrac{m\left(g+a\right)}{k}-\dfrac{mg}{k}.$
Nên li độ lúc sau là: $x+y.$
Ta có: $A^2=x^2+\left(\dfrac{v}{\omega }\right)^2.$
$A^2=\left(x+y\right)^2+\left(\dfrac{v}{\omega }\right)^2.$
Từ đó ta có: $A^2=A^2+y^2+2xy.$
Tính ra: $A=3 \sqrt{5}.$

Đáp án A
+ Tần số góc của con lắc lò xo ω = k m = 50 0 , 2 = 5 π rad/s → T = 0,4 s.
Khi thang máy chuyển động thẳng đều đi lên thì con lắc dao động quanh vị trí cân bằng O′ nằm dưới vị trí cân bằng O ban đầu của con lắc một đoạn Δ l = m a k = 0 , 2.4 50 = 1 , 6 cm và biên độ dao động A = Δl = 1,6 cm.
+ Ta để ý rằng, khoảng thời gian thang máy chuyển động Δt = 20T + 0,75T = 8,3 s → sau khoảng thời gian này con lắc sẽ đi qua vị trí cân bằng O′ → v = vmax = ωA′ = 8π cm/s.
+ Cho thang máy chuyển động thẳng đều, vật lại dao động quanh vị trí cân bằng O với biên độ: A ' = Δ l 2 + v m a x ω 2 = 1 , 6 2 + 8 π 5 π 2 = 1 , 6 2 ≈ 2 , 26 cm.

+ Khi vật đi qua vị trí cân bằng thi biên độ dao động của vật sẽ tăng lên.
Đáp án D

Chọn D
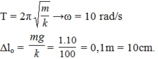
Vật rời khỏi giá đỡ khi phản lực N = 0
Áp dụng định luật II Newton cho vật trên ván chuyển động có gia tốc a, ta được:
mg – N – Fđh = ma
Vật rời ván khi N = 0→Fđh = k.∆l = m(g-a)→∆l = 9cm
Ban đầu ván ở vị trí lò xo giãn 1cm nên khi vật rời ván, ván đi được:
S = ∆l – 1 = 8cm
Khi đó tốc độ của vật ![]() vật cách VTCB là 1cm (chiều dương hướng xuống → x = 1cm)
vật cách VTCB là 1cm (chiều dương hướng xuống → x = 1cm)
=>Biên độ dao động của vật:
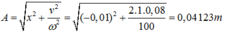

Hướng dẫn:
+ Khi xe chuyển động con lắc đơn sẽ dao động quanh vị trí cân bằng mới, vị trí này dây treo hợp với phương ngang một góc φ 0


Đáp án B
Hướng dẫn:
Ta có thể quy bài toán con lắc lò xo trong thang máy chuyển động với gia tốc về trường hợp con lắc chịu tác dụng của trường lực ngoài F → = F q t → = − m a → .
Để đơn giản, ta có thể chia chuyển động của con lắc thành hai giai đoạn:
Giai đoạn 1: Thang máy chuyển động nhanh dần đều đi lên, con lắc dao động điều hòa quanh vị trí cân bằng mới O′.
Dưới tác dụng của lực quán tính ngược chiều với gia tốc, vị trí cân bằng mới O′ của con lắc nằm phía dưới vị trí cân bằng cũ O một đoạn O O ' = m a k = 0 , 4.4 100 = 1 , 6 cm.
+ Biến cố xảy ra không làm thay đổi tần số góc của dao động ω = k m = 100 0 , 4 = 5 π rad/s → T = 0,4 s.
Thời điểm thang máy bắt đầu chuyển động, vật ở biên trên, do vậy sau khoảng thời gian Δt = 12,5T = 5 s vật sẽ đến vị trí biên dưới, cách vị trí cân bằng cũ O một đoạn 2OO′ = 3,2 cm.
Giai đoạn 2: Thang máy chuyển động thẳng đều, con lắc dao động điều hòa quanh vị trí cân bằng O.
+ Thang máy chuyển động thẳng đều → a = 0, không còn lực quán tính nữa vị trí cân bằng bây giờ trở về O.
→ Con lắc sẽ dao đông với biên độ mới A′ = 2OO′ = 3,2 cm.
→ Thế năng đàn hồi của con lắc cực đại khi con lắc ở biên dưới, tại vị trí này lò xo giãn Δ l m a x = A ' + m g k = 3 , 2 + 0 , 4.10 100 = 7 , 2 cm.
+ Thế năng đàn hồi cực đại E d h m a x = 1 2 k Δ l m a x 2 = 1 2 .100 0 , 072 2 ≈ 0 , 26 J.

Đáp án B
Ta có độ biến dạng của lò xo tại vị trí cân bằng: x = ∆ l = m g k = T 2 g 4 π 2 = 4 c m
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí: x = ∆ l .
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng:
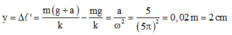
Nên li độ lúc sau là: x' = x + y.
Ta có:
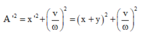
Từ đó ta có:
![]()
Thay số vào ta được:
![]()