Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Có ∆ l = g ω 2 = 1 c m Ban đầu vật có li độ 1 cm và vận tốc 10 π 3 cm/s nên dùng công thức ta có :
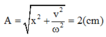
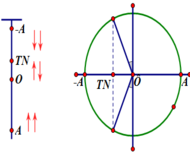
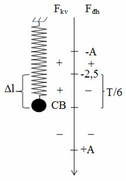
Thời gian lực kéo về và lực đàn hồi lò xo ngược chiều nhau được biểu thị trên hình vẽ. Gọi thời gian đó là t. Dễ thấy thời gian này tạo nên góc quét (hình vẽ) ứng với 60 độ hay T/6
=> t = 1 30 s . Suy ra thời gian lực kéo về và lực đh cùng chiều nhau là 1/6 (s)


Vì lực kéo về luôn hướng về VTCB O, lực đàn hồi luôn hướng về TN (vị trí lò xo có độ dài tự nhiên) nên để 2 lực này ngược chiều nhau, vật phải di chuyển trên đoạn giữa O và TN. 1 chu kỳ vật đi qua đoạn này 2 lần nên suy ra thời gian đi qua đoạn này là T/6
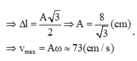

Đáp án A
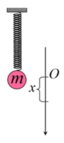
Sau ∆ t 1 lực kéo về triệt tiêu tức là x = 0 (VTCB)
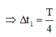
Sau ∆ t 2 lực đàn hồi triệt tiêu tức là lò xo không bi ến dạng
Có
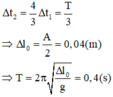

Chọn D.
Tại VTCB độ lớn lực đàn hồi F c b = k ∆ l 0 = m g = 10 N Biên độ
A = ∆ l 0 Chọn gốc tọa độ ở tại VTCB, chiều dương
xuống dưới thì biểu thức lực đàn hồi: F = k ( ∆ l 0 + x )
Tìm các vị trí độ lớn lực đàn hồi 5 N và 10 N:

Thời gian ngắn nhất đi từ -A/2 đến A/2 là T/6.

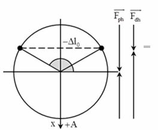
Đáp án A
+ Trong quá trình dao động, lực đàn hồi luôn hướng về vị trí lò xo không biến dạng x = - ∆ l 0 , lực phục hồi hướng về vị trí cân bằng.
+ Trong một chu kì hai lực này cùng chiều nhau là


Đáp án A
Δ l = m g k = T 2 4 π 2 g = 0 , 04 m = 4 c m
Thời gian từ x = 0 → x = + A → x = 0 → x = − A 2 là: T 4 + T 4 + T 12 = 7 T 12 = 7 30 s
Tốc độ trung bình: v = s t = A + A + 0 , 5 A t = 85 , 7 cm/s


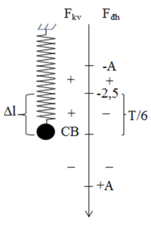

Đáp án A
Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại