Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, đọ cứng 50 N/ m, Khối lượng vật treo là 200 g. Vật đang đứng yên ở vị trí cân bằng thì được kéo thẳng đứng hướng xuống dưới để lò xo giãn tổng cộng 12 cm rồi trả nhẹ cho nó dao động điều hòa. Lấy #Hỏi cộng đồng OLM #Vật lý lớp 12




Đề phải là: Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, độ cứng k = 50(N/m); khối lượng vật treo m = 200g. Vật đang đứng yên ở vị trí cân bằng thì được kéo thẳng đứng xuống dưới để lò xo giãn tổng cộng 12cm rồi thả cho nó dao động điều hòa. Lấy \(\pi^2=10;g=10\left(m,s^2\right)\). Trong một chu kỳ dao động thời gian lực đàn hồi tác dụng vào vật cùng chiều với lực hồi phục là:
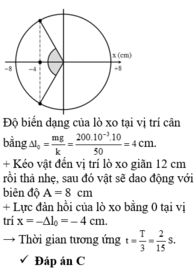
Ta có: \(T=2\pi\sqrt{\dfrac{m}{k}}=0,4s\)
Tại VTCB lò xo giãn 1 đoạn bằng: \(\Delta l=\dfrac{mg}{k}=0,04m=4cm\)
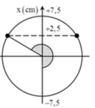
Kéo thẳng đứng xuống dưới để lò xo giãn tổng cộng 12cm rồi thả cho nó dao động điều hòa =>A = 12 - 4 = 8 cm.
Trong một chu kỳ dao động thời gian lực đàn hồi tác dụng vào vật cùng chiều với lực hồi phục là:
t=T/2+T/3=5T/6=1/3s