Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số góc: \(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}=\sqrt{\dfrac{10}{0,04}}=5\pi\) (rad/s)
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)

Đáp án A
*Trong một chu kì lò xo có nén chứng tỏ A > ∆ l o

Chú ý: Lực kéo lớn nhất khi vật ở vị trí thấp nhất (tức là vị trí lò xo giãn nhiều nhất). Lực nén lớn nhất khi vật ở vị trí cao nhất (tức là lò xo bị nén nhiều nhất).

Đáp án A
Trong một chu kì lò xo có nén chứng tỏ

Chú ý: Lực kéo lớn nhất khi vật ở vị trí thấp nhất (tức là vị trí lò xo giãn nhiều nhất). Lực nén lớn nhất khi vật ở vị trí cao nhất (tức là lò xo bị nén nhiều nhất).

Đáp án A
Chu kì dao động của con lắc lò xo T = 2 π ∆ l 0 g = 0,4 s
Ta có:
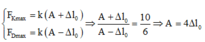
Khoảng thời gian lò xo bị nén trong một chu kỳ ∆ t = T π a r cos ∆ l 0 A = 0 , 168 s

Biên độ: \(A=1cm\)
Tần số góc: \(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}=\sqrt{\dfrac{10}{0,04}}=5\pi(rad/s)\)
Lúc vừa mới thả thì vật đang ở biên, do đó gia tốc của vật là gia tốc cực đại:
\(a_{max}=\omega^2.A=(5\pi)^2.1=250(cm/s^2)\)

Ở VTCB lò xo giãn \(\Delta \ell_0\) thì ta có tần số góc \(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}=\sqrt{\dfrac{10}{0,04}}=5\pi(rad/s)\)
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,4(s)\)
cho mình hỏi, 4cm đó là biên độ đúng không ?