Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

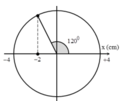
Chu kì của dao động T = 2 π m k = 2 π 0 , 2 10 = 0 , 89 s
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 2.10 10 = 2 c m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên là A 1 = X 0 – x 0 = 6 – 2 = 4 c m .
+ Lực đàn hồi của lò xo là nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng, trong nửa chu kì đầu tiên đối vị trí cân bằng tạm O 1 thì vị trí lò xo không biến dạng có li độ x = –2 cm.
→ Thời gian tương ứng Δ t = 120 0 360 0 T = 0 , 296 s
Đáp án A

Đáp án B
Nên nhớ các công thức trong dao động tắt dần:
Quãng đường vật đi được đến khi dừng hẳn: s = k A 2 2 μ m g
Thay số vào ta được: s = 10 . 0 , 07 2 2 . 0 , 1 . 0 , 1 . 10 = 0 , 245 m = 24 , 5 c m

Sau mỗi nửa chu kì, biên độ của con lắc giảm là:
\(2\dfrac{\mu.mg}{k}=2\dfrac{0,01.0,1.10}{100}=0,0001m=0,1mm.\)
Sau mỗi lần vật qua VTCB thì đúng bằng nửa chu kì, do đó biên độ dao động giảm là 0,1 mm.

Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C

Hướng dẫn: Chọn đáp án C
Cách 1: Độ giảm cơ năng đúng bằng công của lực ma sát:

![]()
Cách 2: Xem I là tâm dao động và biên độ A 1 = A - x 1 , tốc độ tại O:
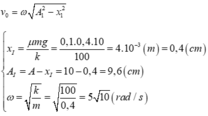
![]()
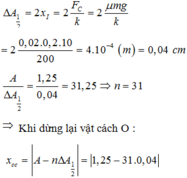


Chọn C
+ Độ giảm biên độ trong nửa chu kì: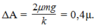
+ Theo yêu cầu của đề: 0,04 + (0,04 – ΔA) < S < 0,04 + 2(0,04 – ΔA)
=> 0,08 – 0,4μ < S < 0,12 – 0,8μ
+ Tới khi dừng hẳn:
+ 0,08 – 0,4μ < 4.10-3 /μ => (μ – 0,1)2 > 0
+ 4.10-3 /μ < 0,12 – 0,8μ => μ2 – 0,15μ + 0,005 < 0 => 0,05 < μ < 0,1.