Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số góc của dao động
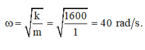
Vận tốc ban đầu chính bằng vận tốc cực đại của dao động
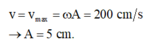
Đáp án A

Chọn B
+ ω = k m = 1600 1 = 40 rad/s.
+ Truyền cho vật vận tốc 2 m/s tại vị trí cân bằng => vmax = ωA = 2 => A = 0,05m = 5cm.

a) Từ định luật bảo toàn cơ năng ta có:
\(\frac{1}{2}mv^2_0=\frac{1}{2}kA^2\)
\(\Rightarrow A=v_0\sqrt{\frac{m}{k}}=2\sqrt{\frac{1}{1600}}=0,05m=5cm\)
b) Phương trình dao động có dạng: \(x=A\cos\left(\omega t+\varphi\right)\)
Tần số góc: \(\omega=\sqrt{\frac{k}{m}}=\frac{1600}{1}=40rad\text{/s }\)
Tại \(t=0\)\(\begin{cases}x=0=A\cos\varphi\\v=-2=-\omega A\sin\varphi\end{cases}\)\(\Rightarrow\varphi=\frac{\pi}{2}\)
Phương trình dao động: \(x=5\cos\left(40t+\frac{\pi}{2}\right)\left(cm\right)\)

Thời gian quả cầu đi từ vị trí cao nhất (x = -A) đến vị trí thấp nhất (x = A) chính là \(\frac{T}{2} = 0,2 => T = 0,4s.\)
Lực đàn hồi của lò xo khi lò xo ở vị trí thấp nhất chính là \(F_{dhmax} = k(A+\Delta l)\)
\(\frac{F_{max}}{P} = \frac{k(A+\Delta l)}{mg} = \frac{kA+k\Delta l }{mg } = 1+\frac{kA}{mg} =\frac{7}{4}\) (do \(k\Delta l = mg\))
=> \(A = \frac{3g}{4}\frac{m}{k} = \frac{3g}{4}.\frac{T^2}{4\pi^2} =0,03m = 3cm.\)
