Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
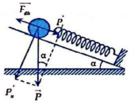
Trọng lực P → được phân tích thành 2 lực thành phần:
![]()
Thành phần P → t nén lò xo, do đó lò xo gây ra lực đàn hồi chống lại lực nén này (định luật III Niuton).
Tại vị trí cân bằng ta có F đ h → cân bằng với P → t
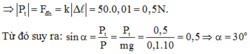

Đenta l(độ dãn của lò xo)=|0,11-0,12|=0,01(m)
Fđh=K*đenta l=50*0,01=0,5N
Fđh=m*g*sin a
=>sin a=Fđh/(m*g)=0,5/(0,1*10)=0,5N=>a=30

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...

Chọn A.
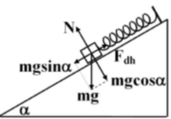
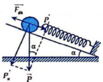
Vật chịu tác dụng ba lực: trọng lực, phản lực và lực đàn hồi.
Ta phân tích trọng lực thành hai phần:
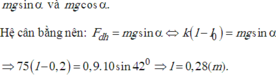

 Đáp án A
Đáp án A
Chọn Ox như hình vẽ
Xét ở vị trí cân bằng các lực tác dụng vào vật bằng O:


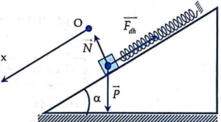
Chọn Ox như hình vẽ
Xét ở vị trí cân bằng các lực tác dụng vào vật bằng O


45 P N F dh
Chọn trục toạ độ như hình vẽ.
Vật ở VTCB lò xo bị nén \(\Delta \ell_0\)
Vật đang đứng yên ở VTCB, hợp lực tác dụng lên vật bằng 0
\(\Rightarrow \vec{P}+\vec{F_{dh}}+\vec{N}=\vec{0}\)
Chiếu lên trục toạ độ ta được: \(P.\sin 45^0-F_{dh}=0\)
\(\Rightarrow mg.\sin 45^0=k.\Delta \ell_0\)
\(\Rightarrow k=\dfrac{mg.\sin 45^0}{\Delta \ell_0}=\dfrac{0,2.10.\sin 45^0}{0,02}=50\sqrt 2(N/m)\)
Chọn C.

+ Xác định độ biến dạng của lò xo
![]()
+ Do bỏ qua mọi lực cản nên cơ năng của con lắc lò xo bảo toàn vậy nó bằng cơ năng ở vị trí bài cho tức là ở vị trí có:
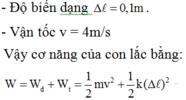
![]()
 10
10


Chọn D.
Trọng lực P ⇀ được phân tích thành 2 lực thành phần:
P ⇀ = P t ⇀ + P n ⇀
Thành phần P t ⇀ nén lò xo, do đó lò xo gây ra lực đàn hồi chống lại lực nén này (định luật III Niuton).
Tại vị trí cân bằng ta có F ⇀ đ h cân bằng với P t ⇀