Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp: Sử dụng vòng tròn lượng giác và định luật bảo toàn cơ năng
Cách giải:
Sử dụng đường tròn biểu diễn vị trí tương ứng M1 và M2 với vật dao động điều hòa khi có li độ M nhưng theo 2 chiều ngược nhau.
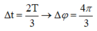
(Cung lớn từ M1 sang M2).
OM1 hợp với trục Ox 1 góc π 3 như hình vẽ
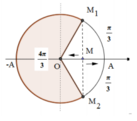
=> Điểm M có li độ x = A/2 = 5 cm
=> Động năng của vật khi đi qua vị trí M là:
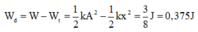
Chọn A
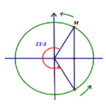
+ E = 1 2 kA2 = 0,5J (nhớ đổi đơn vị của A).
+ Chất điểm ở M nhận cùng một li độ và ngược chiều nhau,ta có hình minh họa. Từ hình vẽ => x = ± A/2.
+ Wđ = 3Wt
(dùng công thức Wđ = nWt ⇔ x = ± A n + 1 )
=> Wđ = 3 4 E = 0,375J = 375mJ.
Đáp án D
Từ thời điểm t đến thời điểm t +
T
4
thì góc quay thêm là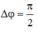 
ở thời điểm t + T 4
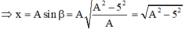luôn có
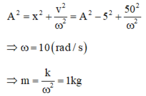
- Từ thời điểm t đến thời điểm t + T/4 thì góc quay thêm là: Δφ + π/2
- Ở thời điểm t + T/4:
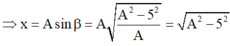
luôn có:
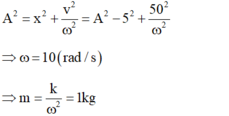
Đáp án D
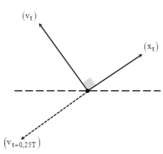
+ Biễu diễn vecto quay cho li độ x và vận tốc v của dao động. Lưu ý rằng tại cùng thời điểm t và v và x vuông pha nhau.
→ Vận tốc của vật tại thời điểm t + 0,25T ngược pha với li độ của vật tại thời điểm t.
→ Với hai đại lượng ngược pha, ta có:
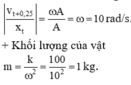
Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\pi(rad/s)\)
Biểu diễn dao động bằng véc tơ quay, tại thời điểm 7/60s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega.t=\dfrac{7}{6}\pi\)
Tại vị trí \(W_đ=3.W_t\)\(\Rightarrow W=W_đ+W_t=4W_t\)
\(\Rightarrow x=\pm\dfrac{A}{2}=\pm 2cm\)
Vì tốc độ của vật đang giảm nên có 2 trường hợp:
+ TH1: Dao động ứng với trạng thái tại M, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên âm --> Li độ là -4cm.
+ TH2: Dao động ứng với trạng thái N, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên độ dương -> Li độ là 4cm.
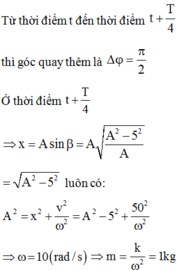
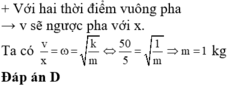
△t=\(\dfrac{5T}{6}=\dfrac{T}{6}+\dfrac{T}{2}+\dfrac{T}{6}\) => S= \(\dfrac{A}{2}+2A+\dfrac{A}{2}\)
=> vị trí M có li độ x=\(\dfrac{A}{2}=5\left(cm\right)\)
=> Wđ =W-Wt=\(\dfrac{1}{2}k.A^2-\dfrac{1}{2}kx^2=0,375\left(J\right)\)