

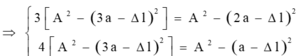
![]()
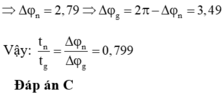
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


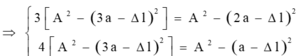
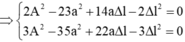
![]()
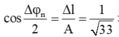
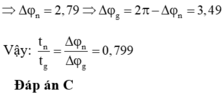

ĐĐáp án C
+ Gọi x1, x2, x3 là li độ ứng với từng vị trí giãn của lò xo.
AÁp dụng công thức độc lập ta được:

Lấy (2) - (1) và (3) - (1) ta được:
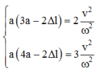
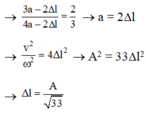
+ Thời gian lò xo nén tương ứng với vật dao động từ vị trí có ly độ Dl đến ly độ -A ứng với góc quét là:
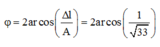
® Thời gian nén là:
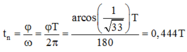
+ Thời gian lò xo giãn là:
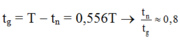

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Bài này có vẻ lẻ quá bạn.
\(W_t=4W_đ\Rightarrow W_đ=\dfrac{W_t}{4}\)
Cơ năng: \(W=W_đ+W_t=W_t+\dfrac{W_t}{4}=\dfrac{5}{4}W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=\dfrac{5}{4}.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{2}{\sqrt 5}A\)
M N O α α
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(\cos\alpha=\dfrac{2}{\sqrt 5}\)\(\Rightarrow \alpha =26,6^0\)
Thời gian nhỏ nhất là: \(\Delta t=\dfrac{26,6\times 2}{360}.T=\dfrac{26,6\times 2}{360}.\dfrac{2\pi}{20}=0.046s\)